No meu último texto, apliquei o modelo Lin-Log. Sem querer buscar neologismos ou novas definições, podemos dizer que o modelo Duplo-log é o irmão siamês do modelo Lin-Log — da família dos semi-logarítmicos. Basicamente, carrega a mesma ideia na modelagem: a adição de logaritmo natural. Mudando aspectos interpretativos e, principalmente, em qual variável aplicar o logaritmo: no Lin-Log, aplica-se o logaritmo às variáveis explicativas do modelo; no Log-Log, aplica-se em todas as variáveis.
Respeitando os pressupostos básicos de regressão, pode-se estimar tanto a versão Log-Log quanto a Lin-Log via Mínimos Quadrados Ordinários (ver, Gujarati & Porter, 2011). Não obstante, lembre-se que a interpretação dos coeficientes estimados difere substancialmente do modelo tradicional de regressão em nível. Assim, o modelo Log-Log em sua versão em regressão simples pode ser representado da seguinte forma:
No qual Yi é a variável dependente, α, o intercepto, β2 é o coeficiente angular da variável independente e, por fim, µi representa o termo de erro. Observe que, como mencionado anteriormente, no modelo Log-Log o coeficiente angular mensura a elasticidade de Y em relação a X, ou seja, a variação percentual de Y dada uma variação percentual em X. O leitor familiarizado com microeconomia básica, imagino eu, conseguiu captar uma das maiores funcionalidades do modelo Log-Log: a elasticidade. Exatamente: o modelo Log-Log consegue captar a elasticidade constante entre as variáveis explicativas e dependentes, a variação em ln Y por unidade de variação em ln X. Dito isso, vamos aos dados.
II — Dados utilizados
Como de costume, as aplicações são, por conveniência, feitas com dados reais. Assim sendo, hoje a aplicação utiliza-se dos dados do Atlas Brasil. Estão disponíveis aqui.
Variável dependente: é a razão entre o somatório da renda de todos os indivíduos residentes em domicílios particulares permanentes e o número total desses indivíduos. Valores em reais de 01/agosto de 2010.
Variável independente: é um subíndice selecionado para compor o IDHM de Educação, representando o nível de escolaridade da população adulta. É obtido pelo indicador % de jovens e adultos com 18 anos ou mais com o fundamental completo. Com todos os estados brasileiros, incluindo o Distrito Federal.
Período: ano de 2010.
III — Rápida análise exploratória
Como manda a tradição, vamos visualizar os dados antes da aplicação e dos resultados obtidos. Inicia-se observando a distribuição e a relação entre as variáveis renda e escolaridade. Observe que, usando todos os estados brasileiros para o ano de 2010, obtemos um modelo em cross-section. Seguem os gráficos.
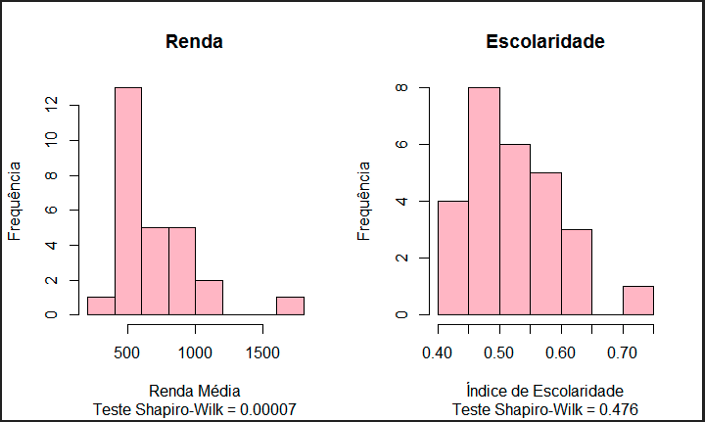
Observe que nos subtítulos estão os resultados do p-valor para o teste de Shapiro-Wilk: sem aplicar logaritmo, a renda não indicou normalidade. Posteriormente, com a aplicação de logaritmo natural, ambas as variáveis retornaram rejeitando a hipótese de não-normalidade. Sobre normalidade e transformação de Box-Cox, veja um texto que escrevi há tempo aqui. Vamos observar de forma mais explícita a relação direcional entre as variáveis aplicando uma correlação de Pearson nas variáveis com Log.
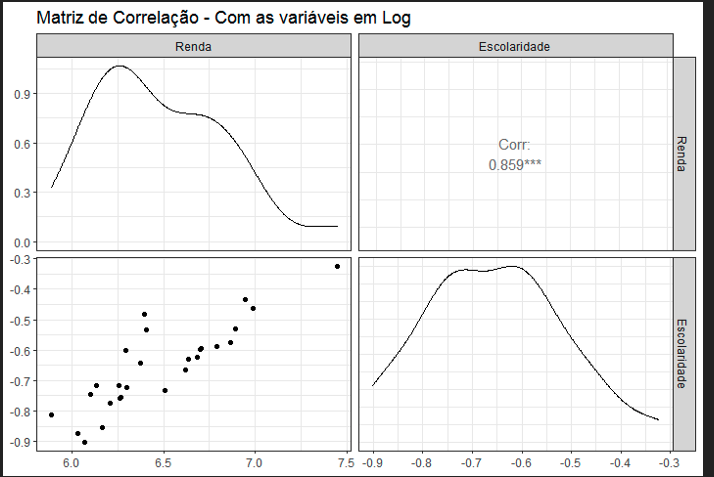
Correlação positiva, como manda a literatura da economia da educação e capital humano. Ok, vamos plotar agora essa relação em apenas um painel com gráfico de dispersão.
Em uma forma menos poluída visualmente (sem log):
IV — Resultados
Poderíamos continuar explorando os dados e, consequentemente, obter informações importantes, mas deixo a cargo do leitor essa parte. Vamos aos resultados e sua interpretação.
Como esperado, a escolaridade retornou estatisticamente significativa a 1% para explicar a renda média — com o coeficiente de determinação de 0.73 e com o F-statistic significante. O coeficiente de escolaridade retornou aproximadamente 2.22. Isso, além de indicar uma relação positiva, indica que o aumento de 1% no índice de escolaridade dos estados, em média, aumenta em 2,22% a renda média dos estados (sendo uma relação elástica).
Não obstante, não custa lembrar que o modelo é apenas um exemplo, o modelo está mal especificado — omitindo variáveis relevantes, aplicando logaritmo em índices, sem ser em dados em painel, amostra pequena, etc. Assim, adicionando um viés nos coeficientes. E, além disso, precisamos fazer alguns testes antes de sair interpretando os coeficientes. A seguir vou optar em visualizar a normalidade dos resíduos do modelo, posteriormente vou aplicar o teste de Durbin-Watson e Breusch-Pagan (para autocorrelação dos resíduos e variância constante):
Como esperado de um modelo mal especificado: os resíduos não têm normalidade e, caso prosseguimos nos testes recomendados na literatura (Greene, 2008), encontra-se que o modelo é heterocedástico e com possível autocorrelação dos resíduos. Em palavras mais simples: os coeficientes estimados indicam inconsistência e viés.
À guisa de conclusão, cabe ressaltar que eu poderia ou “deveria” efetuar o teste de Mackinnon, White e Davidson (1983) para verificar qual a especificação “ideal”: linear ou Log-Log (ou Log-Linear). Novamente, deixo a cargo do leitor, dado meu curto tempo e preguiça proporcionado por um sábado chuvoso. Ah! Diga-se de passagem, para aqueles que quiserem fazer o teste de Mackinnon e companhia, basta fazer o download no R do package petest. Para exemplos, consulte aqui.
Referências
GUJARATI, D. N.; PORTER, D. Econometria Básica. 5th. ed. [S.l.]: McGraw Hill Brasil, 2011.
GREENE, W. H. Econometric analysis. 6th. ed. New Jersey: Practice Hall, 2008.
MacKinnon, J; White, H; Davidson, R. Tests for Model Specification in the Presence of Alternative Hypotheses: Some Further Results. Journal of Econometrics, 1983.
Deixe um comentário