Mercados competitivos – modelo de equilíbrio parcial
Tendo terminado a construção da curva de demanda (link aqui) e a construção da curva de oferta (link aqui) podemos, finalmente, completar o nosso modelo de oferta e demanda. Assim construímos um mercado perfeitamente competitivo baseado nas seguintes hipóteses:
Sem barreiras à entrada
Sem custos de transação
Informação perfeita
Produtores e consumidores atomísticos
Produtos homogêneos
Direitos de propriedade bem definidos.
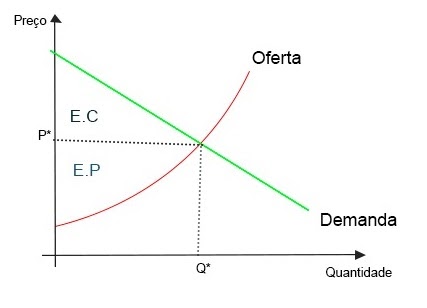
Por maximizar o excedente advindo das trocas econômicas, o mercado competitivo também maximiza o bem-estar. Sendo o bem-estar representado por W, enquanto EC e EP representam os excedentes do consumidor e do produtor, respectivamente. Portanto, tem-se que:
W = EC + EP
Esse bem-estar pode ser representado graficamente da seguinte forma:
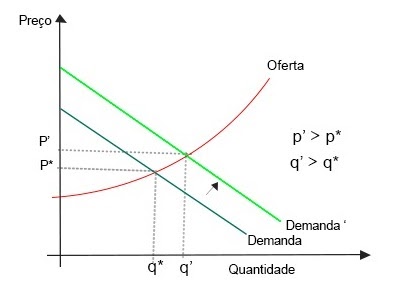
Vamos dar um exemplo da aplicação desse modelo. Vamos assumir um hipotético mercado de sorvetes em pleno verão. Dadas as condições físicas, o calor escaldante do verão faz com que a demanda por sorvetes suba. Ou seja, a disposição dos consumidores a pagar por uma unidade adicional de sorvete aumenta dado o calor ceteris paribus – isto é, tudo o mais constante, a propensão marginal ao pagamento cresce.
Em razão do crescimento da demanda, as firmas vendem mais. Disso se segue maior pressão sobre os preços e sobre a receita marginal da empresa, que, com vistas a maximizar o lucro, tende a se aproximar do custo marginal da firma.
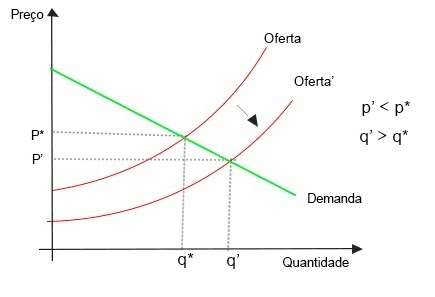
Agora, vamos supor que, após inovações tecnológicas, as sorveterias passam a produzir mais sorvetes a um custo menor. Ou seja, conseguem, assim, produzir mais sorvetes utilizando a mesma quantidade de insumos. De modo a atender um nível mais abrangente de demandantes e maximizar seus lucros, as empresas diminuem os seus preços e os ajustam às novas quantidades demandadas.
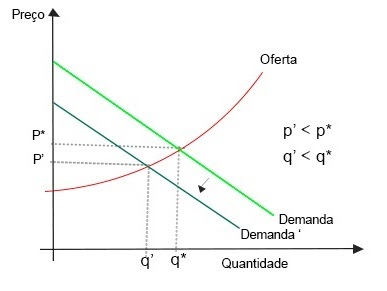
Agora, suponha que o inverno, por conta de suas condições climáticas, tenha retraído a demanda e a disposição marginal das pessoas a comprar uma unidade adicional de sorvete. Ceteris paribus, as firmas, para ajustar-se à nova demanda, são pressionadas a diminuir os preços.
Agora, o cenário final é o de um terremoto na cidade onde a sorveteria comprava seus insumos. Desse modo, tudo ficou mais caro e, para ajustar a oferta, a firma teve de produzir menos a uma mesma quantidade – ou seja, a curva de oferta desloca-se para a esquerda. Para ajustar a nova oferta à demanda, a firma tem que aumentar seus preços.
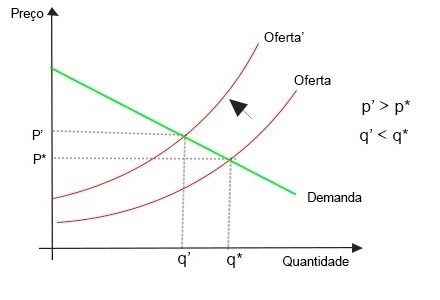
Essas combinações de movimentos das curvas de oferta e demanda esgotam suas possibilidades. Esse modelo, embora simples, não só tem um incrível poder preditivo como pode ser usado para maior variedade de situações. Não à toa, é um modelo basilar para a economia. Mas ainda não está completo. Até aqui, somente observamos os fenômenos interagindo em um mercado – e não como ele reflete os demais. Para isso, nós precisamos de uma análise de equilíbrio geral.
Mercados competitivos – modelo de equilíbrio geral
O problema do consumidor
Vamos considerar para nosso modelo o equilíbrio geral de uma “economia de trocas”, ou seja, por hipótese, que não exista produção.
Definições:
Existem m consumidores
Existem n bens
xji é a alocação do bem i ao indivíduo j
wji é a dotação inicial que o indivíduo j possui do bem i
Xi é a alocação do bem i, i.e, Xi = (x1i, x2i, …, xmi)
X = {X1, X2, … , Xn } é a demanda da economia
Wi é a dotação do bem i, i.e, Wi = (w1i, w2i, …, wmi)
W = {W1, W2, … , Wn }
Alocações factíveis são alocações X tal que: Σmj=1 xji ≤ Σmj=1 wji
Exemplo:
Considere uma economia com dois bens, 1 e 2, e dois indivíduos, A e B.
Alocação de A: xA1 e xA2
Alocação de B: xB1 e xB2
Dotação de A: wA1 e wA2
Dotação de B: wB1 e wB2
As alocações factíveis são dadas por: xA1 + xB1 ≤ wA1 + wB1 xA2 + xB2 ≤ wA2 + wB2
Os agentes têm preferências monotônicas representadas por funções de utilidade côncavas (para saber mais, vá ao apêndice). Podemos representar o conjunto de todas essas alocações factíveis a partir da representação gráfica da caixa de Edgeworth, nas quais suas dimensões representam a quantidade de cada bem.
O ponto W representa as dotações iniciais dos agentes. Em razão das trocas nas quais um melhora sem o outro piorar, as curvas que passam por esse ponto, segundo a lógica de Pareto, não são eficientes. Se unirmos todos esses pontos que exaurem os termos de troca teremos a curva de contrato, que representa todas as alocações Pareto-eficientes. Para encontrar a curva de contrato basta distribuir as dotações originais.
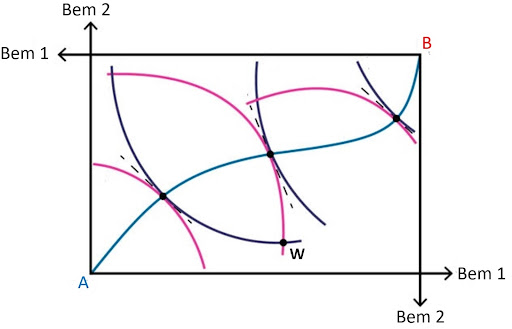
O problema de achar a curva de contrato pode ser matematicamente descrito (de forma simplificada) como:
Tendo resolvido o problema de Pareto, temos a solução de que as taxas marginais de substituição entre os indivíduos devem se igualar. Em benefício da eficiência, essas taxas precisam ser correspondentes.
Agora temos de introduzir o mercado ao problema – ou seja, introduzir os preços relativos dos bens. A taxa de troca (i.e, os preços relativos) é dada, os agentes podem vender a preços vigentes e ir às compras com o dinheiro arrecadado para, assim, monetizar as suas dotações e comprar com o que deriva da operação.
Mas o problema às vezes pode não ter solução. A imagem a seguir representa um problema desse tipo. Existem trocas ainda a serem feitas que maximizam o bem-estar de ambos, sendo uma troca Pareto-eficiente. Nessa situação, vai vigorar um excesso de demanda e um excesso de oferta.
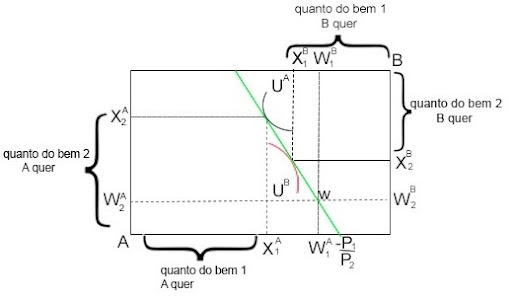
Definição:
Função excesso de demanda individual:
eji = xji (p1, p2, wj) – wji Se eji > 0, temos excesso de demanda. Se eji < 0, temos excesso de oferta.
Função excesso de demanda agregada:
Zi = eAi + eBi = Zi(p1, p2, wAi, wBi)
Se o excesso de demanda vigorar, os preços sobem; já se o excesso de oferta vigorar, os preços caem.
Dados os excessos de oferta e demanda, o Leiloeiro Walrasiano vai alterar os preços, ou seja, as forças de mercado vão agir sobre os preços relativos de tal modo que se chegue ao equilíbrio walrasiano – processo chamado de tâtonnement. Esse processo pode ser representado pela seguinte imagem.
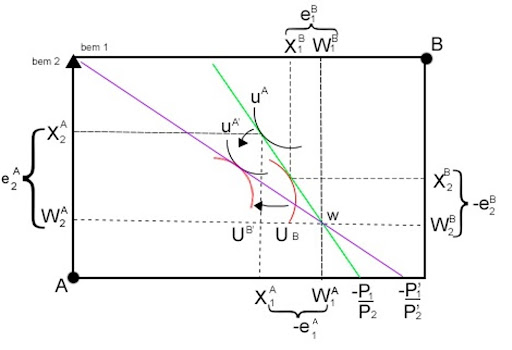
Equilíbrio Walrasiano: é um vetor de preços P*(p*1, p*2) tal que Zi(P*) = 0 para todo i.
Para saber mais do equilíbrio, sua demonstração e propriedades estão no apêndice.
Dado o equilíbrio walrasiano, chegamos ao Primeiro Teorema do Bem-Estar, segundo o qual toda alocação X implicada por um equilíbrio competitivo P* é Pareto-eficiente. Ou seja, de um processo caótico e descentralizado, que é o processo de mercado, deriva um equilíbrio eficiente. A demonstração do Teorema está no apêndice.
O Segundo Teorema do Bem-Estar afirma quetoda alocação Pareto-eficiente pode ser implementada por um equilíbrio competitivo. Esse teorema só é válido se as preferências forem convexas (que é o que assumimos). Isso é válido desde que possamos mudar as dotações a fim de implementar uma alocação Pareto-eficiente.
Deste teorema menos trivial do que eventualmente se supõe deriva o famoso trade-off entre eficiência e equidade, já que é uma situação Pareto-eficiente na curva de contrato aquela em que um indivíduo possui todas as dotações e outro não possui nada. Isto é, esse pode ser um ponto eficiente, mas é socialmente injusto.
A demonstração é demasiadamente longa e complexa para o presente artigo, mas ela pode ser encontrada nas páginas 552-554 do livro “Microeconomic Theory” , de Andreu Mas-Colell, Michael Whinston e Jerry R. Green.
Dado tudo o que foi dito até agora, podemos resolver o problema de mercado dos indivíduos representado acima. A resolução se encontra no apêndice, mas a intuição é que a solução de um mercado competitivo é Pareto-eficiente, ou seja, o primeiro e o segundo teorema são válidos.
O problema da firma
Tendo resolvido o problema para o lado dos consumidores, temos que olhar para as firmas produtoras. As firmas querem produzir da maneira mais eficiente possível, ou seja, usar mais uma unidade de um recurso significa sacrificar mais uma unidade de outro. Neste cenário se está produzindo de maneira eficiente. O cenário de eficiência máxima é aquele representado pela Fronteira de Possibilidades de Produção.
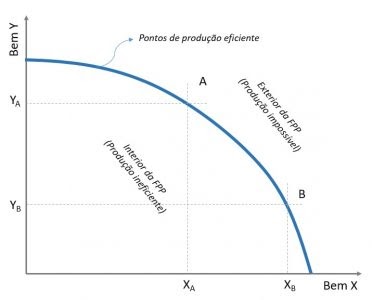
Vamos supor um produto X = Q1 = F1(K,L) e um produto Y = Q2 = F2(K,L). Em ambos bens, tem-se uma função de produção que depende dos insumos K, que representa capital, e L, que representa trabalho. Tendo isso, a fronteira representa todas as possibilidades eficientes de produção. No entanto, o que vai ser efetivamente produzido vai depender dos preços relativos.
Vamos agora introduzir o mercado nesse problema de engenharia de produção. As firmas têm que decidir quanto irão produzir de modo a maximizar seus lucros sujeito às restrições de custos, dados os salários (w) e o preço do aluguel do capital (v). O problema da firma pode ser representado então pela seguinte equação:
maxK,L πi = piFi(Ki,Li) – wiLi -vKi
A resolução do problema pode ser encontrada no apêndice, mas a intuição é a de que a taxa em que se produz de maneira eficiente um produto em termos de outro vai se igualar aos preços relativos, então a produção vai ser justamente um ponto na fronteira de possibilidade de produção, como representa a seguinte imagem.
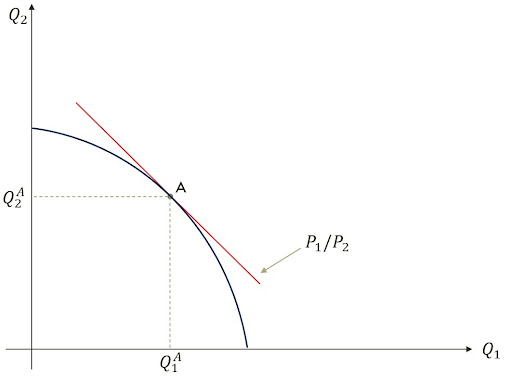
Considerando isso, podemos introduzir o modelo de equilíbrio geral com produção. Não introduziremos as equações, pois seria demasiadamente pesado para esse artigo (que já está pesado em matemática). Logo, nos contentamos aqui com a resolução gráfica. Sabemos que o problema dos consumidores vai ser este:
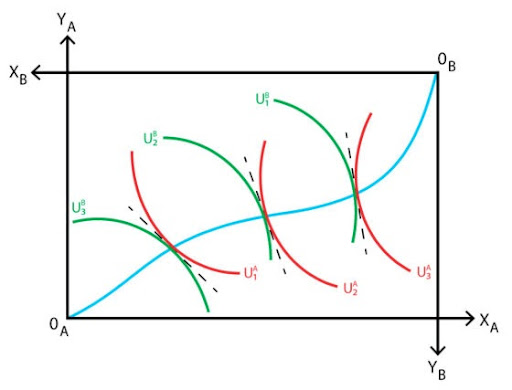
Cuja solução vai ser o vetor de preços p*1/p*2, que zera os excessos de demanda, e é justamente esse vetor de preços que vai se igualar à taxa de produção referida acima, ou seja, ficamos com a seguinte resolução gráfica do problema:
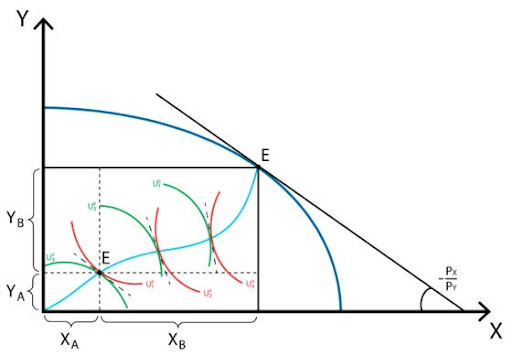
Tendo visto isso, podemos construir a oferta relativa e a demanda relativa. Se o preço relativo do bem 1 aumenta, as firmas que produzem o bem 1 terão um aumento de receita, o que implica que vão produzir mais desse bem em detrimento do bem 2. Ou seja, o setor 1 expande e o setor 2 contrai. Como consequência desse movimento temos uma oferta relativa positivamente inclinada.
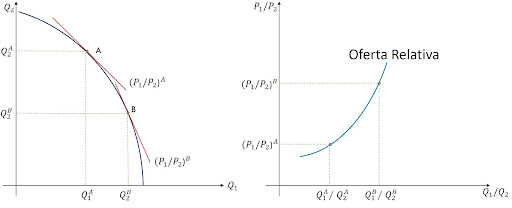
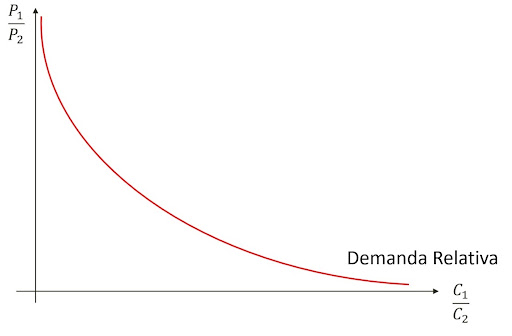
Em relação à demanda, vamos assumir preferências homogêneas e homotéticas (para saber mais dessas propriedades, vá ao apêndice). Os consumidores valorizam os dois bens e a utilidade marginal de um bem vai ao infinito à medida que seu consumo vai a zero. Se p1/p2 aumenta, consumidores querem menos do bem 1 relativo ao bem 2. Portanto, graficamente temos essa demanda negativamente inclinada que não toca os eixos.
Tendo construído a oferta e a demanda relativa, podemos introduzir as duas curvas ao modelo. Os mesmos movimentos da análise parcial valem para as curvas de demanda e oferta relativa. Só que no caso estamos considerando seus efeitos num mercado de dois setores.
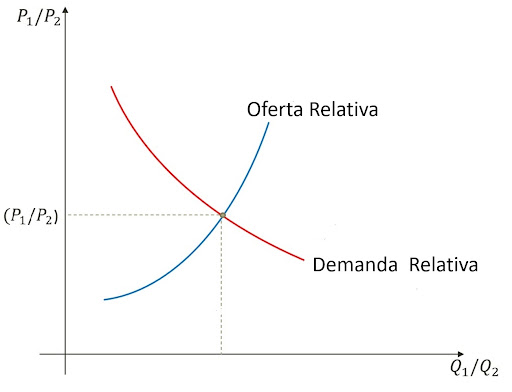
Com isso concluímos o modelo.
Notas sobre o conceito de equilíbrio
O conceito de equilíbrio passa a noção de um estado em repouso, um conceito muito caro à física, que foi tomado emprestado pelos economistas. Economia não é física, nem é uma ciência exata, mas uma ciência social aplicada. É de se esperar que os conceitos de equilíbrio divirjam um do outro.
Para ser justo, a ideia de um equilíbrio como sistema estacionário foi originalmente pensada pelos economistas clássicos. No caso, o repouso significava que as quantidades e os preços dos bens produzidos não mudariam a não ser por choques exógenos. Mas desde a revolução marginalista esse não tem sido o conceito de equilíbrio, que parte, agora, para um estado de natureza no qual os agentes tomam decisões ótimas.
Quem vai elaborar esse conceito de equilíbrio é Hayek em seu paper de 1937 “Economics and Knowledge” e popularizado por Hicks em 1939 no seu livro “Value and Capital”. Segundo afirma David Glasner, no seu artigo “Hayek, Hicks, Radner and Four Equilibrium Concepts: Perfect Foresight, Sequential, Temporary, and Rational Expectations”, Hayek vai pensar num equilíbrio intertemporal que, no lugar de ser pensado como um estado estacionário, privilegia uma visão segundo a qual planos descentralizados ótimos tanto da perspectiva de quem os formula quanto da quem os executa. Os dados subjetivos dos agentes ex ante convergem para os dados objetivos ex post na interação do mercado. Isso faz com que todos os planos dos indivíduos se encaixem. Este conceito de equilíbrio, mais tarde, será expandido e transformado por diversos pensadores. Para saber mais, recomendamos o artigo do Glasner.
Embora adotar essa caracterização hayekiana de equilíbrio sirva ao útil propósito de traçar paralelos reais a esse conceito, também é preciso entender que a economia é essencialmente um conjunto de modelos, e, para cada modelo, há uma definição própria de equilíbrio. Se ele é estável ou instável, se é ou não globalmente estável depende, essencialmente, do modelo a que se reporta o problema.
Equilíbrio, segundo a percepção econômica moderna, nada mais é do que o conjunto de variáveis e/ou pontos que resolvem o modelo. Ele precisa ser entendido usando as variáveis do problema. No caso de equilíbrio geral, trata-se, pois, de uma combinação de fatores, tais como os preços que equilibram o mercado, as decisões das famílias, as decisões de produção das firmas, as decisões que maximizam utilidades e lucros de sorte a não desencadear excesso de demanda. Qual seria o paralelo disso no mundo real? Às vezes, não é preciso que haja um. Equilíbrio, no fundo, nada mais é do que aquilo que resolve o problema — e o comparativo no mundo real depende do modelo.
Apêndice
Definição 1: Preferências monotônicas
A relação de preferência ≽ em R2+ é monotônica se: (i) x1 ≥ y1 e x2 ≥ y2 ⇒ (x1,x2) ≽ (y1,y2) (ii) x1 > y1 e x2 > y2 ⇒ (x1,x2) ≻ (y1,y2)
Definição 2: Preferências convexas
A relação de preferência ≽ em R2+ é convexas se: (i) a ≽ b ⇒ λa + (1 – λ)b ≽ b para todo λ ∈ (0,1)
E estritamente convexa se:
a ≽ b e a =/= b ⇒ λa + (1 – λ)b ≻ b para todo λ ∈ (0,1)
Proposição 1: Caracterização de relações de preferências convexas
A relação de preferência ≽ em R2+ é convexa se e somente se para todo x* ∈ X o conjunto {x ∈ X: x ≽ x*} (contendo todos as cestas pelo menos tão boas quanto x*) é convexo.
Demonstração:
Suponha que ≽ seja convexo. Seja a, b ∈ {x ∈ X: x ≽ x *}. Sem perda de generalidade, suponha que a ≽ b. Então, para λ ∈ (0,1), pela convexidade de ≽ temos λa + (1 − λ)b ≽ b e por sua transitividade temos λa + (1 − λ) b ≽ x*, de forma que λa + (1 − λ) b ∈ {x ∈ X: x ≽ x*}. Portanto este conjunto é convexo.
Agora suponha que {x ∈ X: x ≽ x*} seja convexo para todo x* ∈ X. Se a ≽ b então temos a ∈ {x ∈ X: x ≽ b}. Dado que b também pertence a {x ∈ X: x ≽ b}, a convexidade desse conjunto implica que λa + (1 − λ)b está no conjunto. Assim, λa + (1 − λ) b ≽ b.
C.Q.D
O próximo resultado envolve a noção de uma função côncava. A função u: X -> R é côncava se para todo a, b ∈ X, u(λa + (1 – λ)b) ≥ λu(a) + (1 – λ)u(b) para todo λ ∈ (0,1).
Proposição 2: Preferências com representação côncava são convexas
A relação de preferência ≽ em R2+ que é representada por uma função côncava é convexa.
Demonstração:
Seja ≽ uma relação de preferência representada por uma função côncava u. Suponha que a ≽ b, de modo que u(a) ≥ u(b). Pela concavidade de u,
u(λa + (1 − λ)b) ≥ λu(a) + (1 − λ)u(b) ≥ u(b)
Assim, λa + (1 − λ)b ≽ b, de modo que ≽ é convexo.
Onde TMS é a taxa marginal de substituição, ou seja, quanto de um bem o indivíduo está disposto a sacrificar para ter mais uma unidade do outro bem.
Equilíbrio Walrasiano
Existência: A prova vai além do escopo do presente artigo, mas a resolução se dá pelo fato que se as funções demandas forem contínuas existe ao menos um equilíbrio competitivo. Para a elaboração dessa demonstração recomenda-se Arrow, Kenneth J., e Gerard Debreu. “Existence of an equilibrium for a competitive economy.” Econometrica: Journal of the Econometric Society (1954): 265-290.
Lei de Walras: Se n-1 mercados estão em equilíbrio, então o enésimo mercado também está.
As preferências de um consumidor são chamadas de homotéticas se puderem ser representadas por uma função de utilidade homogênea de grau 1. Por exemplo, em uma economia com dois bens, x, y, as preferências homotéticas podem ser representadas por uma função de utilidade u que possui a seguinte propriedade:
Deixe um comentário