A matemática financeira da aposentadoria

Esse será um texto com bastante álgebra, onde exploro resultados conhecidos da matemática para estruturar o pensamento de quem busca independência financeira na aposentadoria, sem aquele “lenga-lenga” infinito disponível no conteúdo dos influenciadores financeiros do YouTube ou outras redes sociais. Em alguma medida, este post será uma versão resumida e mais matematizada de um texto antigo. O interessante desse post é que ele formaliza uma equação que, se for conhecida ou utilizada por qualquer manual/livro-texto de finanças, não me parece popular até onde eu saiba.

Podemos resumir a matemática financeira da aposentadoria de qualquer pessoa em duas etapas fundamentais. Uma etapa de acumulação e outra no início da aposentadoria de fato, momento em que a única renda disponível do indivíduo é aquela do patrimônio que acumulou. Vamos organizar a conta dessa forma para facilitar a compreensão durante cada etapa. Importante antecipar que todos os fluxos monetários deste exercício estarão expressos em valores monetários corrigidos pela inflação, de forma a simplificar a álgebra.

Etapa 1: Acumulação

Na etapa de acumulação, o trabalhador ou a família (podemos agregar a renda e o patrimônio familiar neste exercício sem perda de generalidade) precisará decidir a parcela da sua renda que ele deverá guardar para que, no futuro, possa sobreviver com o patrimônio acumulado. Logo, podemos enunciar de cara algumas hipóteses.

1. O trabalhador/família vive com renda real média ‘Y’ até se aposentar em um período dado por ‘ $t_1$ ‘;
2. Ao longo do período de trabalho, o trabalhador poupa o montante ‘s’ todo mês ou ano;
3. Sua poupança é integralmente investida em um ativo de renda fixa de retorno real ‘r’ mensal ou anual.

Se definirmos ‘S’ como o valor futuro do patrimônio acumulado após os rendimentos de juros do investimento, sabemos que:

Aqui, ordenamos os aportes em ordem cronológica. O primeiro aporte renderá juros por mais tempo, por isso terá mais peso no patrimônio final. O peso de cada aporte perde relevância ao longo do tempo por este motivo.

S, por acaso, é aquilo que em matemática se conhece por soma dos termos de uma progressão geométrica (PG). Uma sequência de números cujos elementos são multiplicados/divididos por uma razão ‘q’ comum. Há uma maneira bastante elegante de representar essa soma com uma equação curta:

Essa fórmula facilita muito o trabalho de calcular o patrimônio futuro acumulado, bastando substituir os elementos conhecidos. ’n’ é ‘ $t_1$ ’, ‘q’, a depender de como a álgebra é organizada, pode ser (1+r) e ‘ $a_1$ ’ deve ser ‘s(1+r)’ por consistência. Temos então:

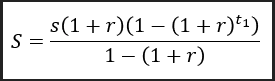
Podemos manipular algebricamente esta equação para simplificá-la da seguinte forma:

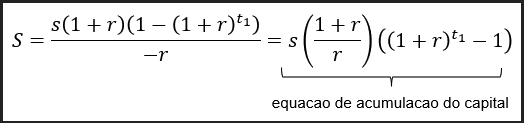
Assim, chegamos na nossa equação final do patrimônio que será acumulado em função do valor poupado ‘s’ e da taxa de juros real sob o qual este investimento foi submetido.

No entanto, uma pergunta vem à mente. Qual é o tamanho ideal do patrimônio a se acumular? É muito comum pensarmos que é possível acumular patrimônio de menos. Mas e se acumularmos demais, sacrificando maior consumo do que gostaríamos por uma poupança que não precisamos? É para isso que serve a Etapa 2.

Etapa 2: Aposentadoria

A etapa de aposentadoria começa no mês seguinte ao último dia de trabalho do indivíduo representativo. Aqui, precisaremos enunciar novas hipóteses:

Trabalhador/família resgatará montante real fixo ‘A’ de sua poupança mensalmente até período ‘ $t_2$ ’;
O restante do capital não resgatado seguirá rendendo o mesmo retorno ‘r’;
A poupança será integralmente consumida de maneira gradual (assim, definimos que a poupança ótima é aquela que o poupador pretende consumir no futuro integralmente).

Para facilitar a interpretação da conta adiante, podemos passar a pensar na contraparte do nosso poupador, que é o banco ou a instituição financeira que pegou seu dinheiro emprestado a juros fixos. Essa contraparte tem uma dívida ‘P’ com nosso poupador, que, a valor presente do momento em que este se aposenta, pode ser representada da seguinte maneira:

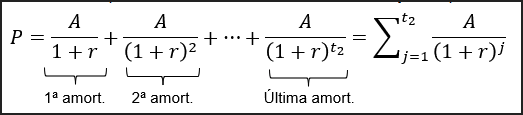
Aqui, temos que o valor presente da dívida é o fluxo de amortizações ‘A’ idênticas trazidas a valor presente pela mesma taxa de retorno que acumulou o patrimônio anterior do nosso poupador.

De maneira muito semelhante à etapa anterior, temos outra soma de uma PG. A PG, dessa vez, tem razão ‘q’ igual a 1/(1+r) e ‘ $a_1$ ’ igual a A/(1+r). Vamos aplicar a fórmula da mesma maneira que na etapa anterior:

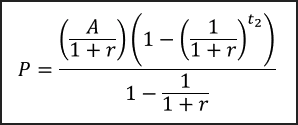
Como na primeira etapa, vamos simplificar essa fórmula e resolver para ‘A’. Ficamos assim:

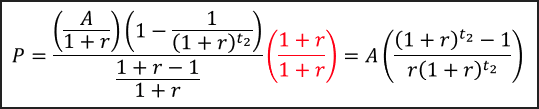
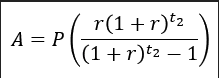
Essa última equação é um resultado famoso para o cálculo de pagamento de dívidas com amortizações constantes, amplamente utilizado por bancos na concessão de empréstimos para pessoas físicas. Aqui, no entanto, vamos dar uma interpretação diferente a ele, esclarecida na última etapa.

Etapa 3: Juntando 1 e 2

Nesta etapa, vamos juntar 1 e 2, igualando ‘S’ a ‘P’. Note que tomamos o cuidado de trazer os dois montantes ao mesmo período no tempo, que é o momento do início da aposentadoria, de forma que estes estejam descritos na mesma unidade (R$ constantes do mês em que o agente se aposentou). Da nossa equação para A, ficamos com:

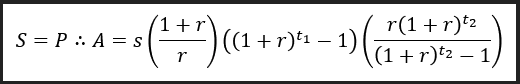
Simplificando a álgebra, temos:

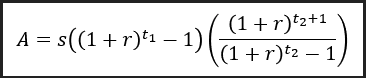
Com isto, encontramos ‘A’, um valor fixo deflacionado de pagamentos constantes mensais em R$ do momento da aposentadoria, que amortiza uma dívida acumulada da contraparte (banco ou instituição financeira) que deverá ser paga ao poupador até o período ‘ $t_2$ ’. ‘A’ é exatamente um benefício previdenciário, um salário que o nosso aposentado resgatará periodicamente até o período ‘ $t_2$ ’ planejado. O período ‘ $t_2$ ’ pode ser definido como o número de anos/meses de sobrevida do nosso poupador. Se escolhermos expressar ‘ $t_2$ ’ em anos, assumindo que nosso poupador se aposenta aos 65 anos de idade e acredita viver até os 90, ‘ $t_2$ ’ = 90-65 = 25 anos.

Além disso, podemos fazer um último ajuste na nossa equação de benefícios previdenciários. Podemos expressá-la a partir de um valor % da renda real média do poupador com algumas definições úteis:

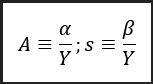
De forma que ‘ $\alpha$ ’ é a renda do aposentado/família como fração de sua(s) renda média real e ‘ $\beta$ ’ é a parcela da renda média real poupada durante o período de acumulação de capital. Logo, temos:

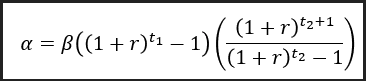
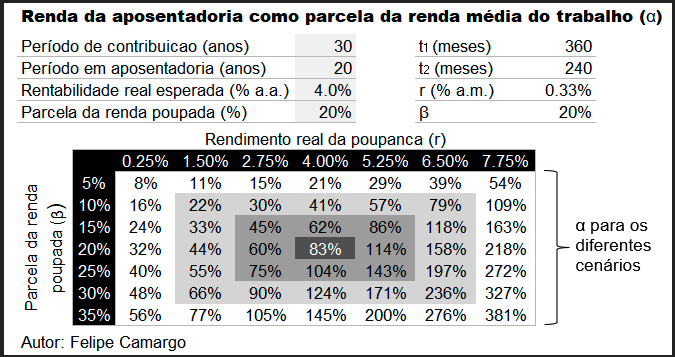
Com esta equação final, chegamos ao resultado que pretendíamos. Podemos simular infinitos cenários para a taxa de reposição da renda na aposentadoria ‘ $\alpha$ ’ em função da parcela da renda que o nosso agente poupou em média ‘ $\beta$ ’ ao longo de ‘ $t_1$ ’ meses/anos, que ele deverá receber por ‘ $t_2$ ’ meses/anos, que também depende da rentabilidade real média mensal/anual ‘r’ de seus investimentos. Segue um exemplo prático na matriz abaixo.

Considerações finais

Como em meu post anterior sobre planejamento financeiro, esclareci que o acúmulo de patrimônio é uma função da poupança, do tempo e do retorno. Aqui, isso fica muito mais claro e resumido para os que conseguem ler a álgebra apresentada. Como de costume, deixarei uma planilha com todas as etapas algébricas e as simulações apresentadas para os que tenham se interessado e queiram refazer o exercício com base em seus próprios parâmetros.

Publicado originalmente aqui.