No texto anterior, simulamos aleatoriamente dois países que possuem uma relação específica e usamos de especificações econométricas para “desvendar” tais relações de forma satisfatória em uma infraestrutura de equação única.
Relembrando onde paramos, exploramos uma ideia de dois países fictícios, Atlântida e Conchinchina, onde o segundo possui forte relação exógena e de longo prazo com o primeiro.
Nossa relação observada nas duas economias simuladas em computador.
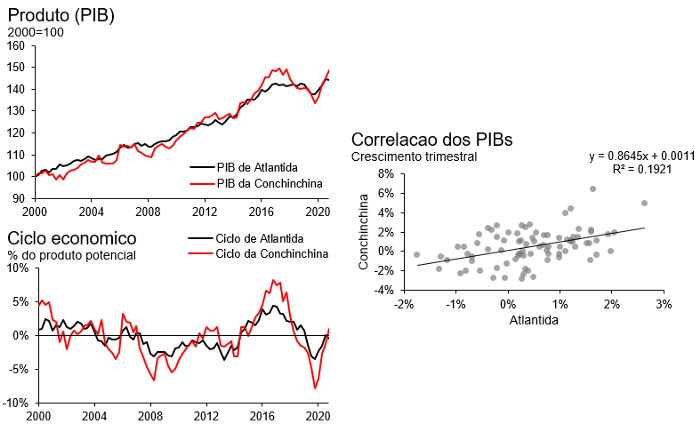
Na primeira parte, experimentamos uma primeira especificação econométrica, essa de livro-texto, e enxergamos com gráficos o motivo pelo qual tal modelo, apesar de bem especificado, falha em capturar uma relação de longo prazo que definimos mas ficou faltando. Nosso modelo MQO simples nos provia uma projeção onde o PIB da Conchinchina divergia ao longo do tempo em relação a Atlântida.
Após isso, encontramos uma forma de representar dinâmicas de curto e longo prazo com modelos de regressão em nível com lags. Regressões com lag dificultam em parte a interpretação estatística dos testes de correlação entre as variáveis, em razão destas possuírem tendência, mas de forma alguma nos impede de fazê-la. Passamos rapidamente pela questão da cointegração entre as variáveis, e como sua presença era o que nos permitia usufruir de tal modelo. No presente texto, a cointegração e um pouco de álgebra será o elo que permitirá a união entre as relações de curto e longo prazo em um modelo econométrico de equação única.
Vamos começar este novo modelo a partir do último modelo que usamos e analisamos na parte 1, o modelo ARDL(1,1):
O modelo ARDL(1,1) é aquele que regride variáveis I(1) e/ou I(0) com variáveis explicativas I(1) e/ou I(0). As notações 1,1 se referem a um lag de variável dependente y(t-1) e um lag de variável independente x(t)+x(t-1).
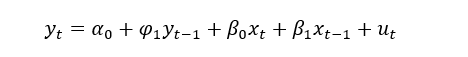
Para chegarmos onde queremos chegar, vamos fazer algumas manipulações algébricas simples neste modelo, conforme abaixo:
Primeiro, tomamos a primeira diferença de y em ambos os lados da equação.
Aqui, adicionamos e subtraímos β0x(t-1) para transformar x(t) em uma primeira diferença e somarmos um novo coeficiente em x(t-1) em nível.
No passo seguinte, decompomos o intercepto pela soma de dois interceptos diferentes (o motivo disso ficará claro no passo seguinte). Note que ao longo dos passos fomos agregando e deixando em evidência os novos coeficientes de cada equação.
Aqui, ao passarmos todos os termos de x em nível e da constante decomposta para dentro do termo entre parêntenses de (1-φ1), e chegamos a uma forma funcional final. Note que o termo em roxo é parecido com o que foi encontrado na primeira parte.
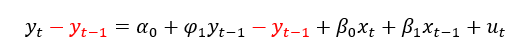
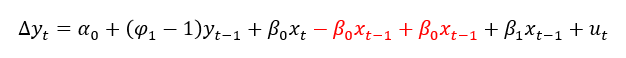
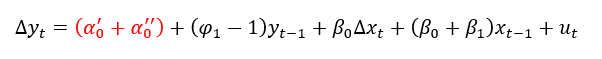
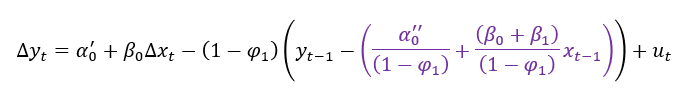
No primeiro texto deduzimos os coeficientes de longo prazo do nosso modelo ARDL(1,1) da seguinte forma:
Note que a forma funcional destes coeficientes sao idênticas às que encontramos no nosso modelo novo.
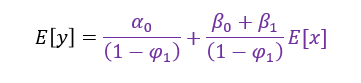
O leitor pode não ter percebido, mas nesta manipulação algébrica deduzimos o que é conhecido como um modelo de correção de erros (ECM). Este modelo é bastante popular na sintetização de relações exógenas de curto e longo prazo entre variáveis, além de eliminar alguma parte das dificuldades de identificação estatística que possuíamos no modelo ARDL anterior, por se tratar de uma regressão final em primeira diferença.
O modelo ECM.
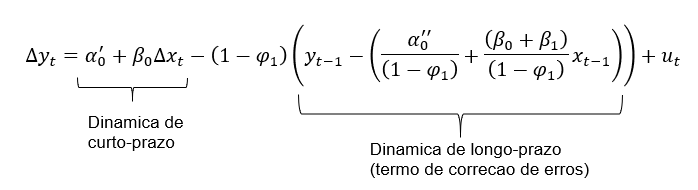
Para implementar este modelo, podemos simplesmente assumir que a relação entre os coeficientes em nível y e x é:
Neste modelo, assumimos que α e β são simplesmente parâmetros que resumem toda a relação de variáveis da manipulação algébrica anterior.
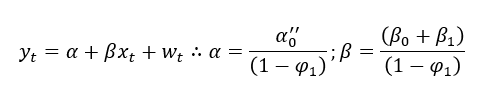
Assim, estimamos uma primeira equação, que mede os coeficientes de longo prazo do nosso modelo:
Vale notar que nosso coeficiente regredido em nível aqui conforme a especificação acima nos resultou em um β para x estatisticamente igual ao do modelo anterior, dentro do intervalo de um desvio-padrão somente.
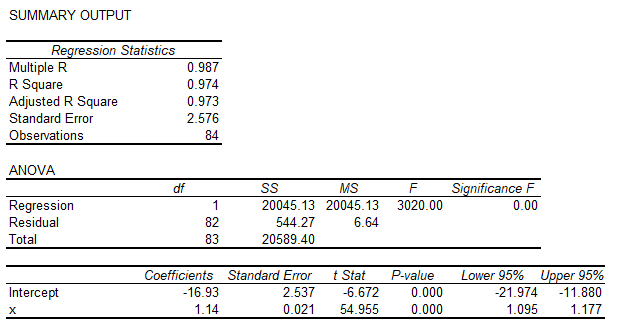
De posse deste modelo, usaremos o resíduo w da regressão com uma defasagem, uma vez que sabemos que este resíduo é exatamente o termo de longo prazo:
A estacionariedade do resíduo é o indicativo de que y e x cointegram.
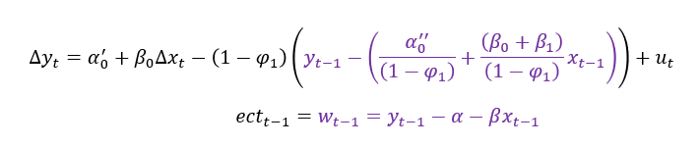
Podemos entao regredir a equação acima com a simples especificação:
Aqui, para simplificar, substituímos os termos de φ1-1 por λ para simplificar a notação. Para que o modelo faça sentido e de fato haja uma correção gradual dos desvios da dinâmica de longo prazo especificada, é necessário que -1 < λ < 0.
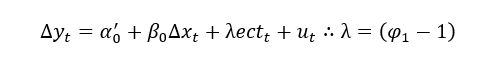
Ao extrairmos os resíduos da primeira regressão para a segunda, agora em um modelo em primeira diferença, temos:
Note que nos livramos do problema anterior, onde as estatísticas-teste da regressão em nível eram espúrias. Temos um R² e estatísticas-t confiáveis.
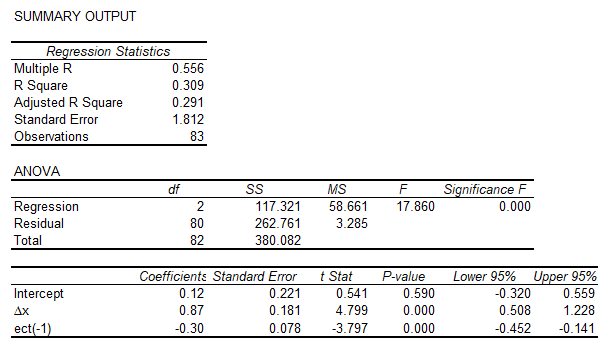
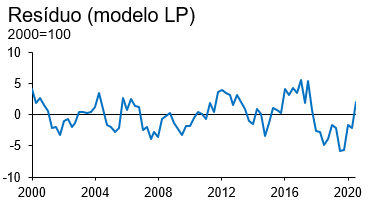
O output do modelo, conforme veremos, é basicamente um espelho dos resultados do modelo ARDL, uma vez que se trata basicamente de uma manipulação algébrica de coeficientes estatisticamente idênticos. Para facilitar a visualização, plotei os dois resíduos em conjunto no gráfico abaixo. Eles ficam quase que completamente sobrepostos.
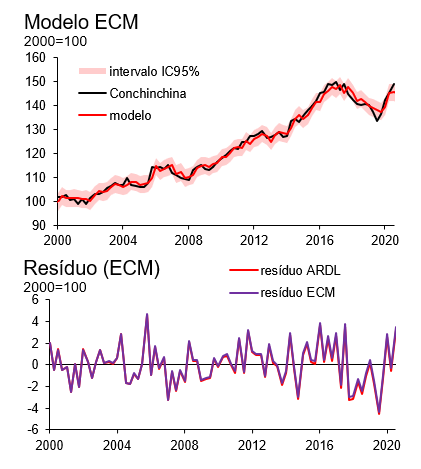
A forma funcional do nosso modelo, no entanto, agora está muito mais explícita e visível do que antes, o que nos permite inferências mais intuitivas sobre a dinâmica do PIB da Conchinchina diante de mudanças no PIB de Atlântida:
Nosso modelo final, após estimação, com seus coeficientes centrais.
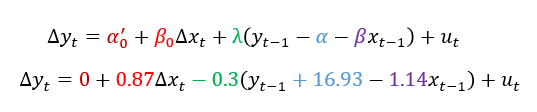
A maior vantagem deste modelo, no fim das contas, é finalmente nos proporcionar uma dinâmica cujo output explica, consistentemente, o ritmo de crescimento e o nível do PIB de Conchinchina pelo ritmo de crescimento e o nível do PIB de Atlântida.
Na imagem, observamos que as variações entre os dois PIBs convergem ao longo do tempo, e as economias agora divergem a uma diferença percentual constante em nível dada pelo coeficiente β de longo prazo.
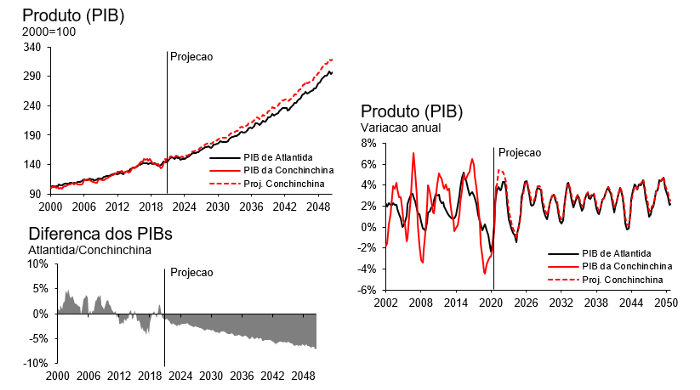
Dessa forma encerro esta série, onde ilustro o poder dos modelos ECM, sua relação intrínseca com modelos ARDL, que regridem variáveis em nível, não somente em primeiras diferenças. Através de diferentes etapas, compreendemos que há um pouco além da econometria do que aquilo que os livros-texto ensinam, e que muito pode ser desvendado com um pouco de exercício prático (obviamente, não tudo). Espero que tenham gostado.
Deixe um comentário