Esse é o terceiro e último texto da série sobre finanças e análise de investimentos. Leia aqui a parte 1 e aqui a parte 2.
No último texto desta série, encerramos o assunto aprendendo como enxergar e pensar no conceito de risco: para que serve calcular um desvio-padrão e o Beta dos retornos de diversos ativos; o que significam os valores desses paramêtros e o que esperar deles ao longo do tempo. O que não aprendemos, no entanto, é como estruturar essas informações para fazer escolhas – o que, no fundo, é o que eu chamei de “administrar risco”.
Em teoria do portfólio abordamos a escolha de um investimento arriscado como uma escolha sob incerteza. Para simplificar, a teoria define que investidores possuem o que chamamos “graus de aversão ao risco”, e essa aversão ao risco é definida por uma ideia de que investidores racionais exigem “prêmios” em retornos mais altos para julgar razoável a escolha de investimentos mais arriscados.
Isso é bastante intuitivo. Pense da seguinte forma: se alguém te oferecesse duas oportunidades de investimento, uma com 50% de chance de dar $100 de prejuízo mas com 50% de chance de dar $300 de lucro, ou outra oportunidade com $100 de lucro garantido, é natural entender que a grande maioria das pessoas preferirá a segunda oportunidade ao invés da primeira, apesar de ambas terem igual valor esperado.
Com base nessa lógica foi criada a teoria da utilidade dos portfólios, que basicamente define uma função com certas propriedades matemáticas desejáveis, por hipótese, para tentar estruturar como pensa uma pessoa que lida com escolhas de diferentes investimentos arriscados. A forma funcional de enxergar essa escolha de portfólios arriscados é definida de muitas formas, mas para fins de didática escolherei uma bastante simples aqui, ilustrada na equação abaixo.
u(r) é a função utilidade associada ao retorno esperado E[r], um coeficiente de aversão ao risco “A” e o risco deste retorno esperado σ.
A utilidade (satisfação) por escolher um determinado investimento é definida como função da sua expectativa de retorno descontada do risco deste retorno esperado multiplicado por um coeficiente de aversão ao risco subjetivo, denotado por “A”. Na prática, a disponibilidade de investimentos com informações públicas acessíveis (como ações em bolsa, títulos públicos, moedas e derivados destes) facilita bastante a ideia de um consenso de mercado a respeito do retorno esperado e do risco desses investimentos (afinal, foi exatamente o que fizemos no texto anterior).
De posse de parêmetros como E[r] e σ para estes ativos, basta então medirmos o coeficiente “A”, subjetivo por definição. Cada um de nós tem uma sensibilidade diferente ao risco, que pode ser matematicamente capturada por este parâmetro, conforme a ilustração gráfica abaixo:
Curvas de indiferença são as diferentes combinações de retorno e risco que proporcionam a mesma utilidade (satisfação) para um investidor com determinado nível de aversão ao risco (A).
Como pode ser visto pelas diferentes trajetórias de retorno no eixo vertical para mudanças idênticas no risco, um investidor racional vai exigir um aumento exponencial de seu retorno para manter-se indiferente a um aumento cada vez maior de risco. Um investidor com um coeficiente A de 7 somente aceitará um investimento com 20% de risco se este investimento oferecer um retorno esperado de 22% (ou seja, 22% em média, mas que poderia ficar entre -18% e +62% com 95% de confiança). Enquanto isso, um investidor com coeficiente A de 3 toparia este mesmo nível de risco com um investimento de retorno esperado bem mais baixo, de 10% (portanto, 10% de média, mas podendo chegar a -30% e +50% com os mesmos 95% de confiança).
Note que mesmo considerando ambos os investidores avessos ao risco, esses podem ter graus de aversão ao risco diferentes, e por isso racionalmente exigir maior “prêmio” em retornos esperados para correr a mesma unidade a mais de risco. A melhor forma de se compreender qual a aversão ao risco de alguém, portanto, é perguntando a esse potencial investidor quanto ele exigiria a mais de retorno para correr um dado valor adicional de risco, e é assim que toda a teoria de escolha ótima de portfólios é construída.
A compreensão do conceito de utilidade na relação risco x retorno é fundamental porque permite unificar uma teoria que engloba tanto a ideia de retorno requerido (obtido através do cálculo do planejamento do patrimônio desejado ao fim de um determinado número de anos de poupança e investimento, que derivamos no primeiro texto dessa série) e do risco máximo tolerado (medido através da volatilidade e Beta dos retornos do texto subsequente). Agora podemos trabalhar com tudo isso com a intenção de construir um portfólio adequado para cada um, um portfólio que vai consistir em uma combinação de ativos diversificados que ofereçam um nível de risco e retorno compatível com os objetivos patrimoniais e tolerância ao risco de cada investidor.
Chegou, finalmente, o momento de falar dos benefícios da diversificação; como usá-la em favor do investidor que tem uma boa ideia de quanto de retorno precisa e de quanto risco está disposto a tolerar no caminho da acumulação do seu patrimônio. Vamos primeiro ilustrar esse benefício graficamente e depois discutir porque ele acontece, matematicamente.
A combinação em vermelho de dois ativos com correlação negativa e tendência positiva gerou um portfólio com um retorno intermediário, porém muito mais desejável em termos de relação risco x retorno.
Como podemos ver no gráfico acima, ao comprarmos isoladamente ações da empresa X ou da empresa Y, teríamos feito algum retorno ao longo do tempo, correndo bastante risco. Essa combinação entre ativos negativamente correlacionados torna possível preservar um determinado nível de retorno correndo menos risco. E por mais que se possa argumentar que o investimento em Y possa ter sido muito mais vantajoso em retorno, conforme vimos acima, esse pode ainda assim não ser um ativo razoável para um investidor avesso ao risco.
É sempre preciso ponderar risco e retorno, afinal, mais risco é o preço justo que o mercado nos exige por maior retorno. Pensando nisso, muitos financistas gostam de normalizar retornos pelo seu risco, criando índices, como o Índice Sharpe. Com o índice, podemos pensar na eficiência de um determinado investimento a partir de quantas unidades de retorno a mais ele adiciona para cada aumento em seu risco. Com base na maximização deste índice, é possível definir a quantidade e a proporção ótimas dos ativos em um portfólio racional.
O Índice Sharpe é a razão entre o excesso de retorno do portfólio arriscado (p) sobre o retorno livre de risco (rf) e a volatilidade (σ) do retorno do portfólio.
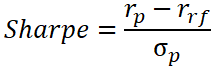
Então agora já podemos falar um pouco mais sobre como funciona esse processo de otimização. Neste momento, vou propor um exemplo numérico para tornar mais ilustrativo, e com base nele reforçarei alguns dos conceitos pincelados anteriormente.
Nesta relação hipotética de retorno, os ativos Y e Z são virtualmente idênticos em risco e em retorno, apesar de ao mesmo tempo possuírem um correlação distinta com ativo X. Isso será um ponto importante adiante.
Aqui, temos a opção de escolher entre 2 ativos arriscados para combinar com X (X com Y ou X com Z), e depois combinar essa carteira de ativos arriscados com nosso ativo de renda fixa. Para construir essa carteira, montarei um gráfico das relações risco vs retorno para cada uma das proporções destes ativos arriscados em um portfólio.
A fronteira eficiente, o coração da teoria de portfólio moderna.
No gráfico acima, a fronteira eficiente é destacada em vermelho por ser justamente a região de combinações entre X e Y onde todos os seus pontos são superiores em retorno à região da curva em preto, com retornos inferiores e risco idêntico. Isso significa que investir na região preta seria irracional (ou, como a própria fronteira diz, ineficiente). O Índice Sharpe das combinações de X e Y é maximizado no ponto destacado da região vermelha da fronteira, onde alocamos 65% do patrimônio investido em Y e o restante em X. Esse índice maximizado nos oferece um portfólio de retorno de 7.3% com risco de 17.7% (inferior, portanto, ao risco de qualquer um dos ativos isolados, com um retorno razoavelmente acima do ativo menos arriscado oferecido).
Vamos comparar agora o mesmo gráfico contra uma diversificação de X com o ativo Z, que possui risco e retornos idênticos a Y porém mais correlacionado com X que Y.
Nas combinações entre ativos mais correlacionados, podemos notar que apesar de ainda haver um benefício de diversificação, esse benefício é bastante reduzido.
Em virtude dessa maior correlação entre X com Z do que entre X com Y, todas as combinações entre X e Y são superiores às combinações entre X e Z. Isso acontece porque o benefício da diversificação é sempre maior quanto menor for a correlação entre ativos. Esse fator é bastante importante quando pensamos em montar uma carteira diversificada, uma vez que é perfeitamente possível adicionar novos ativos em uma carteira e não obter tantos benefícios de diversificação assim. Uma carteira pode estar mais diversificada com 3 ou 4 ativos do que uma carteira com 30 ou 40, a depender da correlação dos ativos que estão dentro dela. O risco de uma carteira diversificada com dois ativos pode ser medido da seguinte forma:
Cálculo do desvio-padrão de uma carteira com dois ativos correlacionados, X e Y. O componente de correlação é denotado pelo termo ρxy. O parâmetro “a” é o peso associado à proporção do ativo naquela carteira.
Na equação acima, podemos pensar que o risco de uma carteira diversificada é composto pela soma dos componentes de risco de cada um de seus ativos (denotados em cinza e em vermelho na fórmula acima) acrescidos ao produto cruzado entre eles (sua correlação, denotada em roxo). Em uma carteira com 2 ativos há somente um componente de correlação (no caso do exemplo, a correlação entre X e Y), mas se incluíssemos um novo ativo Z, teríamos 3 (entre X e Y, entre X e Z e entre Y e Z), e assim subsequentemente. O resultado disso é que após alguma diversificação dilui-se o benefício de se acrescentar um novo ativo na carteira, e uma carteira pode estar perfeitamente diversificada com poucos ativos a depender da correlação entre eles.
Esse processo também pode ser feito e aperfeiçoado através de tentativa e erro, bastando que o investidor calcule a volatilidade passada de cada ativo em separado e comparando com as multiplas possíveis combinações de retorno entre estes ativos. O resultado deve ser o mesmo.
Bom, agora que entendemos o processo de otimização de um portfólio arriscado, vamos seguir adiante com o passo de combinar este portfólio com um ativo livre de risco. A razão pela qual fazemos isso é que desta forma encontramos todas as combinações possíveis de uma carteira com Índice Sharpe idêntico, em uma reta que chamamos de Capital Market Line.
Capital Market Line é a linha de maximização do Sharpe da carteira arriscada com a renda fixa.
A Capital Market Line é a linha que permite ao investidor incorporar a sua tolerância ao risco com seu retorno requerido. Um investidor estaria igualmente confortável em termos de retornos eficientes (os níveis de Sharpe são os mesmos), mas esse nível de retorno eficiente precisará se encontrar com aquela curva de indifença que traçamos no primeiro gráfico do texto.
O portfólio ótimo é aquele que tangencia a curva de indiferença entre risco e retorno previamente definido do investidor avesso ao risco.
O portfólio ótimo é aquele onde o investidor encontra o ponto tangente entre a sua curva de indiferença e a reta de combinações eficientes de um portfólio diversificado combinado com a renda fixa. Dessa forma, unificamos em um equilíbrio ótimo toda a teoria de escolha de portfólios, onde o investidor decide por um retorno requerido para construir seu patrimônio, analisa os ativos que tem à sua disposição para fazer seu investimento, diversifica-os, obtém uma relação de risco x retorno ótima e escolhe a combinação que melhor se adequa ao seu grau de aversão ao risco.
E por aqui eu fico com a minha série de textos sobre como estruturar investimentos de forma racional. Acredito que a principal lição deste conteúdo é passar a ideia de lembrar que risco é um custo no momento de decidir investir (o preço pelo maior retorno), e precisa ser tratado como tal. Volto a lembrar que o conteúdo sobre investimentos nas redes sociais hoje é bastante amplo, mas geralmente muito raso, e passado por pessoas que não estão expostas ao órgão que regula as boas práticas na hora de discutir investimentos.
Espero que o material ajude os novos investidores a entender que o trabalho dos gestores profissionais de carteiras de investimento é de uma profundidade muito maior do que o que estes influenciadores de internet nos levam a acreditar. Nada vai te proteger melhor de conselhos ruins do que a sua força de vontade em aprender as nuances por trás do uso do seu dinheiro na formação de patrimônio.
Deixe um comentário