O modelo IS-LM é o primeiro modelo de curto-prazo ensinado nos cursos de macroeconomia de graduação. No entanto, apesar do seu ensino extensivo, ele não pode ser considerado como intuitivamente representativo da forma como as questões macroeconômicas são tratadas atualmente, principalmente em relação a operacionalização da política monetária. Nesse sentido, enquanto a construção do modelo IS-LM é fundamentado assumindo a oferta de moeda — ou a taxa de crescimento da oferta de moeda — como constante, implicando que a taxa básica de juros se ajusta aos choques na economia, a macroeconomia orientada pela Nova Síntese Neoclássica assume a taxa de juros como constante e a oferta de moeda se ajustando aos choques na economia, de modo a manter a taxa de inflação estável.
Porém, isso não significa que o modelo tenha perdido o seu valor. Apesar de pouca utilidade prática, o modelo possui utilidade didática e de aprendizado. Ou seja, ao entender o seu funcionamento, o estudante exercita a capacidade de abstração e entendimento da forma como fenômenos macroeconômicos podem ser modelados matematicamente.
Antes de nos aprofundarmos propriamente no modelo, cabe contextualizar a sua finalidade. Como dito anteriormente, o modelo IS-LM é um modelo de curto-prazo. Isso significa que o seu objetivo é entender os efeitos na produção (Y), dada a modificação em alguma de suas variáveis exógenas — política monetária e fiscal —, assumindo que o nível de preços permanece constante.
Dessa forma, devido à existência de imperfeições de mercado, principalmente no mercado de fator trabalho, as firmas não ajustam instantaneamente os preços para qualquer variação na demanda pelos produtos ofertados. Sendo assim, o estímulo/desestímulo ao consumo (C) e ao investimento (I) — através da operacionalização da política monetária e fiscal — provoca variações do nível de produto real da economia, alterando principalmente o nível de emprego do fator trabalho (L) no processo produtivo.
Graficamente, o modelo é representado da seguinte maneira:
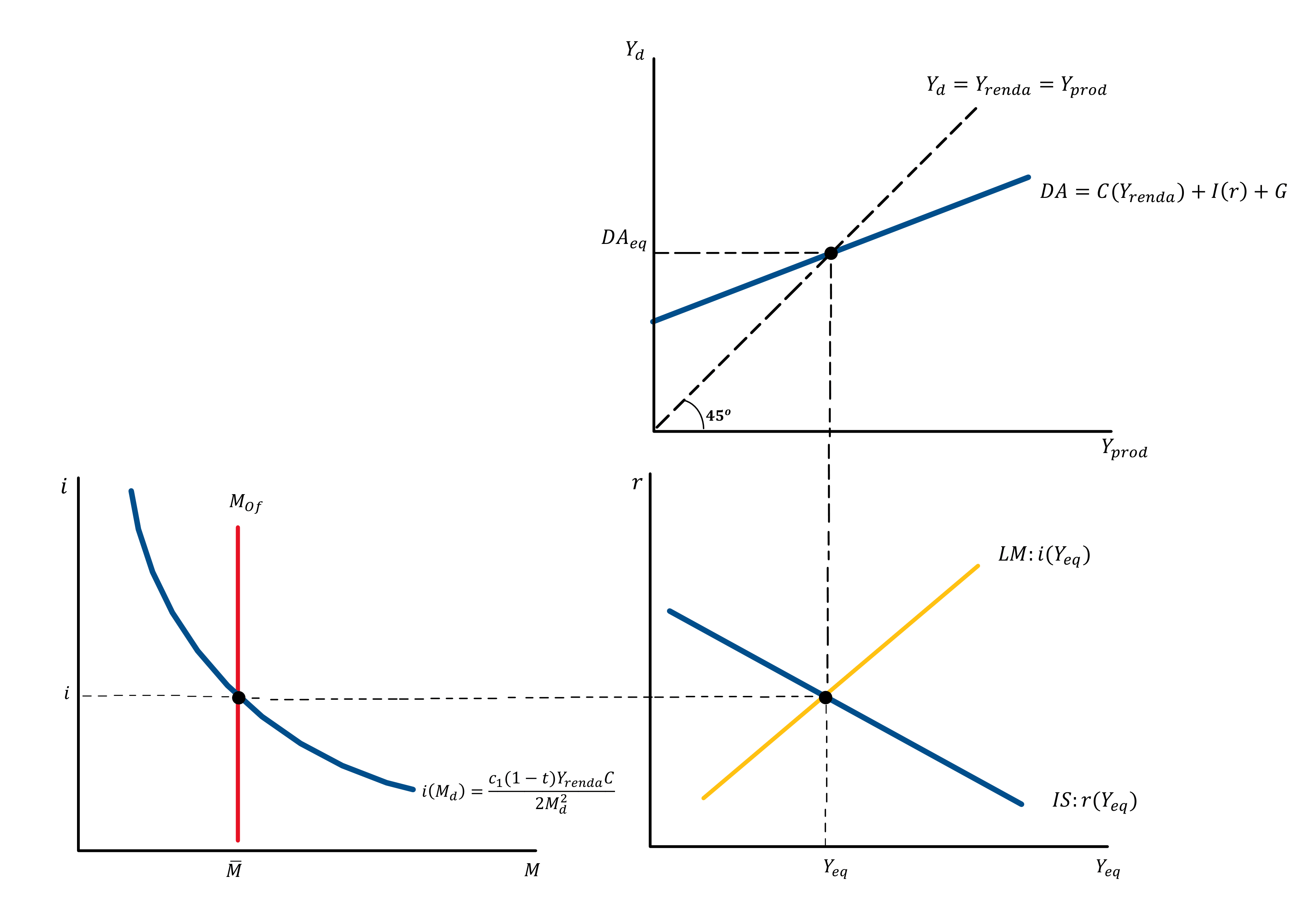
O gráfico do canto superior direito representa o equilíbrio no mercado de bens, quando a demanda é igual à produção de bens e serviços e o investimento (I) é igual a poupança (S). O gráfico no canto inferior esquerdo representa o equilíbrio no mercado monetário/financeiro, quando a demanda ótima de moeda para motivo transacional é igual a oferta exógena de moeda determinada pela autoridade monetária.
Já o gráfico do canto inferior direito representa o equilíbrio simultâneo entre o mercado de bens, através da curva “IS” (em que o nível de investimento (I) é influenciado pela taxa de juros de equilíbrio (r) no mercado monetário), e o mercado monetário, através da curva “LM” (em que a demanda ótima de moeda por motivo transação é determinada pelo produto de equilíbrio (Y) no mercado de bens).
O entendimento dessas interrelações fica mais evidente após a dedução formal do modelo, que será feita a seguir.
2. O lado da demanda: a curva IS
Começaremos deduzindo o lado da demanda da nossa economia por dois motivos. Primeiro, o equilíbrio no mercado de bens é uma condição para a ocorrência do equilíbrio no mercado monetário. A ideia é que o equilíbrio no mercado de bens determina a necessidade de demanda de moeda pelo motivo transação — o que será explicado na terceira parte do texto —, sendo uma das condições necessárias para a determinação do equilíbrio da curva LM. Segundo, o sentido econômico por trás da construção da curva IS é muito mais intuitivo do que o da curva LM.
O ponto de partida da dedução da curva IS se dá pela apresentação da identidade contábil de mensuração do PIB pela ótica da despesa:
em que: Y_d: Despesa agregada; C: Consumo das famílias; I: Investimento agregado; G: Gastos do governo; X: Exportações; M: Importações; (X-M): Balança de bens e serviços.
Como neste texto trataremos de uma economia fechada, podemos desconsiderar o saldo na balança de bens e serviços. Dessa forma, temos o seguinte ponto de partida:
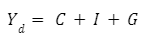
A modelagem econômica será feita atribuindo hipóteses comportamentais para os componentes de consumo agregado (C) e investimento agregado (I) da identidade acima. A intuição por trás é a de imaginar os fatores determinantes do comportamento de cada um desses componentes, de modo a elaborar uma equação que explique o que acontece com o nível agregado, dada a variação dos parâmetros ou variáveis explicativas da equação.
2.1. Modelando o consumo agregado (C)
Por exemplo, uma das formas de incorporar o comportamento do consumo agregado é através da função de consumo keynesiana:
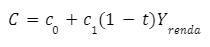
em que: C: Consumo agregado; c_0: Consumo autônomo; c_1: Propensão marginal a consumir (PMC); t: Proporção de imposto de renda; Y_{renda}: Renda agregada das famílias.
O entendimento dessa equação é bem simples. O primeiro termo do lado direito representa a parte do consumo que independe da renda das famílias e que, como estamos falando de um comportamento agregado, podemos entendê-lo como sendo o consumo de subsistência financiado por programas de redistribuição de renda, por exemplo, ou o consumo gerado por renda de ativos financeiros previamente acumulados. O segundo termo representa a parcela da renda (Y_{renda}) direcionada ao consumo, após a dedução da alíquota de imposto (t). Também é assumido que a propensão marginal a consumir (c_1) é um valor entre 0 e 1. Ou seja, nem toda a renda é consumida/poupada; parte é consumida e parte é poupada.
A intuição dada pela função de consumo keynesiana é a de que, no agregado, o consumo é uma função estável e diretamente relacionada com a renda das famílias. Ou seja, se a renda das famílias aumenta, o consumo aumenta na proporção do valor da PMC; se a renda das famílias diminui, o consumo diminui na proporção do valor da PMC. Além disso, podemos entender que a alíquota de imposto (t) sobre a renda das famílias financia os gastos do governo. Já o resíduo não consumido e não direcionado ao financiamento do governo é a poupança da economia.
Graficamente, a função de consumo keynesiana é representada da seguinte forma:
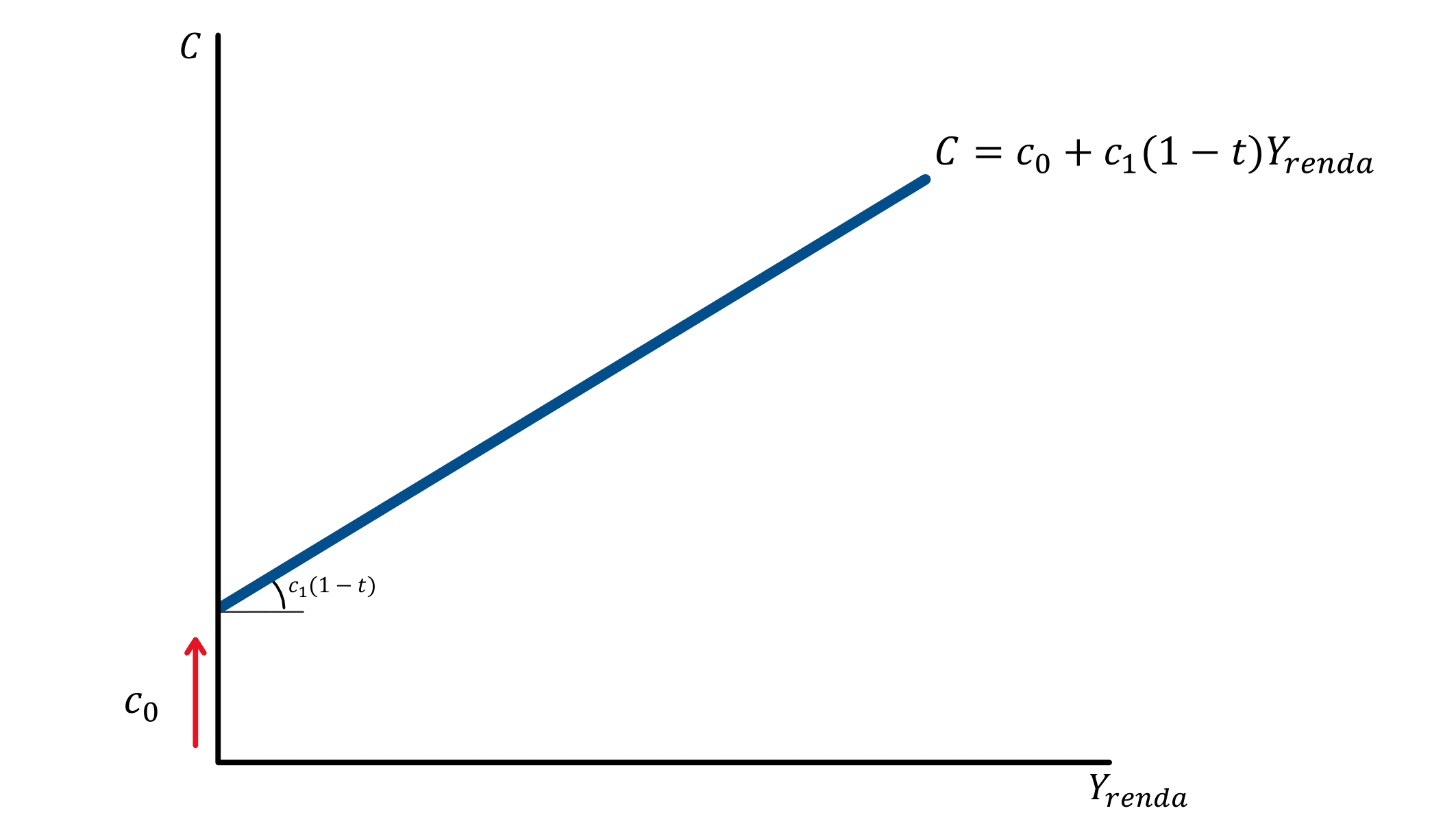
2.2. Modelando o investimento agregado (I)
A modelagem do investimento agregado (I) é mais simples, e pode ser feita da seguinte maneira:
em que: I: Investimento agregado; a_0: Investimento autônomo; a_1: Elasticidade do investimento em relação à taxa de juros; r: Taxa de juros real.
A intuição desse modelo de investimento, dado o sinal negativo no segundo termo (que gera uma inclinação negativa no gráfico I vs. r), é a de que quanto maior a taxa de juros real, menor será o investimento da economia e, de forma análoga, quanto menor a taxa real de juros, maior será o investimento da economia. Em relação ao investimento autônomo, os manuais de macroeconomia de graduação o consideram como sendo uma simplificação da parcela do investimento que depende do nível de renda da economia, cujo tratamento é desenvolvido apenas em tópicos mais avançados.
Graficamente, a função de investimento pode ser representada da seguinte maneira:
Agora que modelamos os componentes do consumo agregado (C) e do investimento agregado (I), podemos continuar com a derivação da curva IS.
2.3. Derivando a curva IS
A derivação da curva IS ocorre a partir da introdução dos modelos dados pelas funções de consumo e investimento na equação de mensuração do produto pela ótica da despesa:
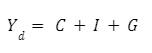
Substituindo a função de consumo keynesiana no componente de consumo agregado (C) e a função de investimento no componente de investimento agregado (I), temos:
Entender essa equação é importante, pois é a partir dela que é deduzido o efeito multiplicador de gastos, impulsionando o resultado de equilíbrio dada a variação em algum dos componentes autônomos da despesa agregada. A dedução do efeito multiplicador é feita assumindo que, no equilíbrio, a renda das famílias é igual à despesa agregada e ao produto da economia. Ou seja, a condição de identidade contábil de Contas Nacionais é satisfeita:
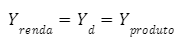
A partir da relação acima, podemos representar o equilíbrio da equação de demanda agregada (DA) no diagrama da cruz keynesiana:
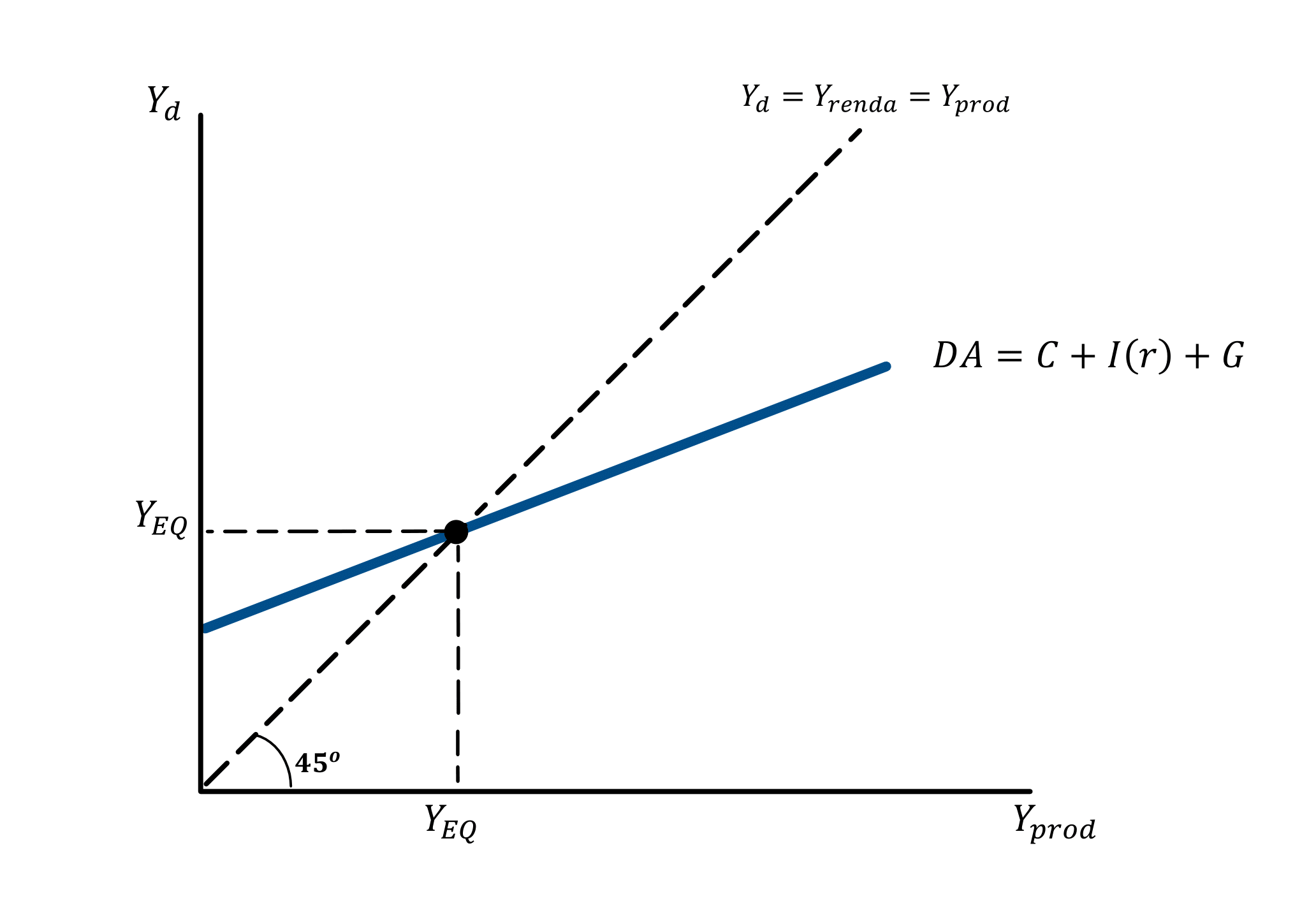
Conforme colocado anteriormente, o resultado de equilíbrio é obtido devido à identidade de mensuração do Produto Interno Bruto (PIB), de modo que há igualdade entre as óticas de Renda, Produção e Despesa. Percebam que em nenhum momento foi modelado o comportamento da produção da economia (oferta). Isso ocorre pois a produção é assumida como endógena ao modelo do multiplicador, e o equilíbrio é alcançado pois a identidade é necessariamente verdadeira.
Nesse sentido, para encontrar o produto de equilíbrio, basta colocar Y em evidência, portanto, igualando despesa e renda:
O resultado acima representa a renda de equilíbrio da economia, em que o nível de despesa agregada iguala o nível de renda agregada, de modo que o primeiro termo do lado direito da igualdade representa o efeito multiplicador. Como 0 < c_1 < 1, então o multiplicador necessariamente assume um valor superior a 1. Ou seja:
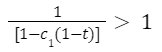
De maneira implícita nesse resultado está que a produção real da economia responde sempre na mesma proporção da variação da demanda agregada (DA), mas que é limitada pelo fato de que a PMC é inferior a um. Por exemplo, poderíamos imaginar o que aconteceria se a PMC tendesse a 1. Nesse caso, o multiplicador tenderia ao infinito. Isso pode parecer um absurdo, mas ocorre pois está implícito que a capacidade de oferta da economia no curto-prazo sempre atende as necessidades da demanda agregada (DA).
Como na curva IS a taxa de juros da economia está em função do produto de equilíbrio, para deduzi-la basta resolvermos a equação para a taxa de juros, encontrando o seguinte resultado:
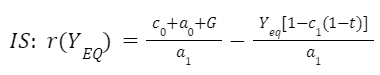
A equação acima pode ser graficamente representada da seguinte maneira:
Podemos entender o que acontece com o gráfico dada uma variação positiva em algum dos componentes autônomos da curva de despesa agregada, principalmente os que podem ser controlados pela política monetária (taxa de juros) ou pela política fiscal (gastos do governo). Uma variação positiva nos gastos do governo (G) desloca tanto a curva de despesa agregada quanto a curva IS, sendo graficamente representada da seguinte maneira:
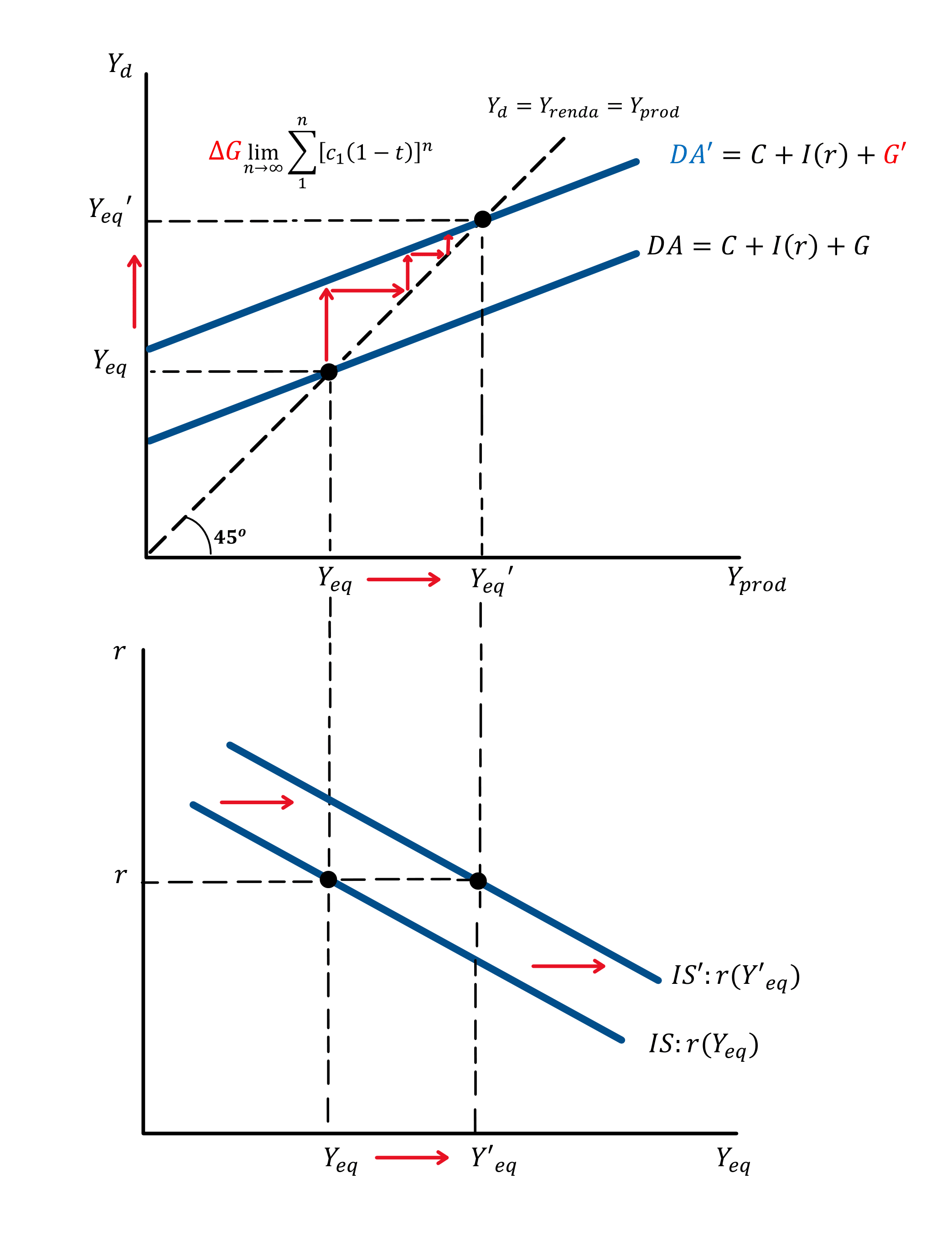
A intuição por trás do gráfico é que um aumento dos gastos (\Delta G > 0) do governo provoca um aumento da demanda e, portanto, um aumento da necessidade de produção da economia. As firmas, para suprirem a nova demanda, contratam mais trabalhadores. O aumento do nível de emprego provoca um aumento da renda e novamente o aumento da demanda, posteriormente, gera um novo aumento da produção e novamente do emprego. O ciclo se repete até que o novo ponto de equilíbrio seja encontrado. Essa dinâmica somente faz sentido assumindo que os preços são rígidos no curto prazo, pois, caso contrário, as firmas poderiam apenas elevar os preços dos produtos.
Já uma variação da taxa de juros (r), ao variar o nível de investimento agregado (I), desloca a curva de despesa agregada, e provoca um movimento ao longo da curva IS. Uma redução da taxa de juros (r) pode ser representada graficamente da seguinte maneira:
Da mesma forma que um aumento nos gastos do governo, uma redução da taxa de juros provoca um aumento da despesa agregada (portanto, um aumento na necessidade de produção da economia). As firmas, para suprirem a nova demanda, contratam mais trabalhadores. O aumento do nível de emprego provoca um aumento da renda e novamente o aumento da demanda, posteriormente, gera um novo aumento da produção e novamente do emprego. O ciclo se repete até que o novo ponto de equilíbrio seja encontrado. Em caso de variação negativa nos gastos do governo (\Delta G < 0) ou positiva na taxa de juros (\Delta r > 0), a mecânica de funcionamento é a mesma, mas em direção contrária.
Agora que sabemos a mecânica de funcionamento da determinação do equilíbrio no mercado de bens, podemos entender como funciona a determinação do equilíbrio no mercado monetário a partir da dedução da curva LM, de modo a tornar endógeno a taxa de juros (r).
3. O lado monetário: a curva LM
Enquanto a curva IS identifica a relação entre taxa real de juros (r) e nível de renda (Y) que proporciona o equilíbrio no mercado de bens, a curva LM apresenta a taxa de juros que equilibra o mercado monetário/financeiro para uma determinada oferta de moeda fixa e nível de renda da economia. Dessa forma, a interseção entre as duas curvas proporciona a taxa de juros que equilibra simultaneamente o mercado de bens (portanto, o nível de investimento da economia) e o mercado monetário/financeiro (portanto, a taxa de juros que representa o custo de oportunidade de reter moeda em termos da taxa de juros de equilíbrio entre os ativos da economia).
No caso teórico básico, a decisão de alocação financeira é feita considerando a existência de apenas dois ativos: moedas e títulos. Enquanto títulos são demandados por renderem juros, a demanda por moeda é justificada pelos seguintes motivos: transação, precaução e especulação/portfólio.
O motivo transação decorre da necessidade dos agentes econômicos manterem uma certa quantia de moeda em caixa para fazer frente às necessidades transacionais de fluxos de caixa diários. Podemos citar o exemplo de um comércio comum, que mantém um montante de dinheiro na caixa registradora com o intuito de liquidar as operações realizadas com clientes e fornecedores, seja para pagamento de boletos ou para retornar em troco a diferença entre a o valor da cédula e o valor da compra. Para o modelo IS-LM, o motivo transação é diretamente proporcional à renda agregada da economia e é considerado como sendo a única justificativa racional e eficiente para se demandar moeda.
O motivo precaução pode ser considerado como um subgrupo do motivo transação, e é justificado pela possibilidade de surgimento de necessidades transacionais não previstas, como, por exemplo, o defeito em algum equipamento ou um acidente, que, para ser solucionado rapidamente, é necessário ter moeda em estado máximo de liquidez.
Por fim, o motivo especulação/portfólio é justificado pelas perspectivas dos agentes em relação ao comportamento futuro da taxa de juros dos títulos da economia.
Dessa forma, por envolver decisões de alocação de ativos, para entender a análise que sustenta a dedução da curva LM é necessário ter um conhecimento básico de precificação de ativos. Para a finalidade do texto, podemos considerar que a economia é composta por um único título, denominado perpetuidade. A perpetuidade é um tipo de ativo financeiro cujo seu detentor tem o direito de receber um fluxo de rendimento constante ao longo do tempo de maneira perpétua. A sua precificação ocorre a partir do cálculo do somatório dos fluxos de rendimentos futuros descontados a uma determinada taxa, que pode ser a taxa de um determinado ativo alternativo e de mesmo risco. Ou seja:
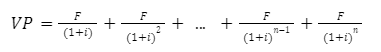
em que: VP: Valor presente (preço) da perpetuidade; F: Fluxo de rendimentos da perpetuidade; i: Taxa de desconto; n \rightarrow \infty é o período.
Ou seja, o preço de um título perpétuo é o somatório dos fluxos de rendimentos futuros descontados pelo custo de oportunidade de um título alternativo de mesmo risco.
Para solucionar essa progressão geométrica infinita e de razão inferior a um, começamos colocando o fator de desconto em evidência:
Podemos substituir o VP da primeira equação na segundo, da seguinte forma:
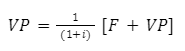
Manipulando algebricamente, o resultado final fica:
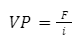
Neste texto, como a decisão de alocação é entre moeda e título, em última instância, a taxa de desconto é representada pelas preferências dos agentes entre reter moeda pelo motivo especulação ou aplicar em títulos. Portanto, como no modelo IS-LM a oferta de moeda é fixa, mudanças súbitas nas preferências dos agentes econômicos em relação ao comportamento da taxa de juros (i) provoca mudanças no nível de retenção de moeda — ou seja, o motivo especulação/portfólio —, tendo como efeito variações no preço do título.
Sendo assim, se há um choque de pessimismo (incerteza em relação aos investimentos) na economia, de modo que há um aumento generalizado na retenção (demanda por moeda) a partir da venda de títulos, isso implica uma redução no preço dos títulos e, como o fluxo de rendimento (F) é constante, um aumento da taxa de desconto (i):
Dessa forma, como a curva LM no caso mais simples representa o equilíbrio no mercado monetário/financeiro, a taxa de juros (i) que prevalece da relação entre esses dois mercados é aquela em que as expectativas em relação ao seu comportamento estão ancoradas, logo não há motivo especulação/portfóliopara se demandar moeda. Sendo assim, a demanda por moeda é somente a necessária para satisfazer o motivo transação, que é considerado pelo modelo IS-LM básico — em situações normais — como sendo o único motivo racional e eficiente para se demandar moeda, sendo este exatamente os pontos sobre a curva LM.
Os manuais de macroeconomia normalmente sintetizam a dedução da curva LM da seguinte forma. Temos uma oferta de moeda exógena, controlada pela autoridade monetária, e uma equação que representa a função de demanda de moeda pelo motivo transação. A retenção de moeda é determinada pela renda da economia, na proporção do parâmetro k — que é a constante marshalliana —, e é influenciada pela taxa de juros (i), na sensibilidade dada pelo parâmetro h.
Respectivamente:
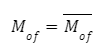
Graficamente, o resultado de equilíbrio é representado da seguinte maneira.
O diagrama do lado esquerdo do gráfico acima representa o equilíbrio no mercado monetário/financeiro para uma curva de demanda por moeda linear e uma oferta de moeda exógena. O diagrama do lado direito apresenta a curva LM e mostra os pontos de equilíbrio entre taxa de juros (i) e nível de renda (Y), mantendo a oferta de moeda fixa. Dessa forma, uma variação positiva no nível de renda (Y) necessariamente eleva a taxa de juros (i) de equilíbrio no mercado monetário/financeiro.
Apesar do resultado acima parecer satisfatório — afinal, a forma funcional da função de demanda por moeda relaciona tanto o motivo transação quanto a influência da taxa de juros (i) de mercado sobre a retenção de moeda —, quando analisado com um pouco mais de cuidado, algumas contradições acabam surgindo. Por exemplo, se considerarmos uma situação em que a taxa de juros (i) de equilíbrio seja máxima, de modo que a oferta de moeda é zero, então as famílias não realizam transações econômicas, de modo que o produto não pode ser positivo.
Além disso, embora haja uma fundamentação teórica, não há uma explicação econômica — no sentido de custo de oportunidade — para os valores atribuídos aos parâmetros k e h, bem como não há uma definição precisa a respeito de qual motivo de demanda de moeda o componente com a taxa de juros (i) está se referindo. Alguns manuais argumentam como sendo o motivo especulação/portfólio, já outros dão a entender como sendo uma parte da demanda por moeda destinada ao motivo transação influenciada pela taxa de juros (i), no sentido de ser uma simplificação do modelo Tobin-Baumol.
No entanto, com um tratamento um pouco mais aprofundado e formal a respeito do motivo transação para se demandar moeda, grande parte dos questionamentos e possíveis contradições são explicados. É o que veremos a seguir.
Os modelos de demanda por moeda para motivos de transação podem ser subdivididos em duas categorias: a visão clássica, tomando a equação de trocas como forma de identificação da demanda, mas que independe da taxa de juros; e a visão keynesiana, tomando o modelo de alocação de estoques de Tobin-Baumol, em que a demanda por moeda depende das necessidades transacionais dos indivíduos e da taxa de juros. Vamos analisar cada uma dessas visões.
3.1. O motivo transação — A visão clássica
A visão clássica da demanda por moeda para o motivo transação está intrinsecamente relacionada com a equação de trocas:
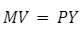
em que: M: Quantidade de moeda; V: Velocidade de circulação da moeda; P: Nível de preços; Y: Produto/renda da economia.
Resolvendo a equação acima para M, temos:
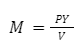
Em que M pode ser considerado uma função de demanda por moeda pelo motivo transação, e o inverso da velocidade de circulação da moeda a constante marshalliana (k), ou seja, a proporção da renda que é direcionada para satisfazer as necessidades transacionais da economia:
A lógica é a seguinte. Imagine que um indivíduo representativo recebe um salário de $ 5.000,00, depositado em uma conta-corrente num banco comercial num mês de 30 dias. Desse montante, 20% é destinado ao pagamento do imposto de renda e outros 20% é alocado numa poupança de longo-prazo. Sendo assim, a quantidade total de moeda em caixa do indivíduo representativo é de $ 3.000,00.
Nessa economia, a moeda física é o único meio de pagamento aceito como intermediário do processo de trocas. Além disso, a sociedade é extremamente segura, de modo que não há motivos para que o indivíduo representativo mantenha os $ 3.000,00 de renda salarial líquida em conta-corrente. Portanto, como existe a inconveniência de ter que ir ao caixa eletrônico para sacar qualquer quantia de moeda física, e não há incentivos para manter qualquer quantia em conta-corrente, o indivíduo representativo saca os $ 3.000,00 no mesmo dia em que recebe a sua renda mensal, e esse valor é gasto em consumo de maneira contínua ao longo do mês.
Quando o indivíduo representativo está em posse dos $ 3.000,00 em moeda física, isso significa que ele tem um “encaixe”, “saldo monetário” ou “retenção de moeda” de mesma quantia (nos manuais de macroeconomia e economia Monetária, esses termos são intercambiáveis).
O comportamento financeiro do indivíduo representativo é representado graficamente da seguinte forma:
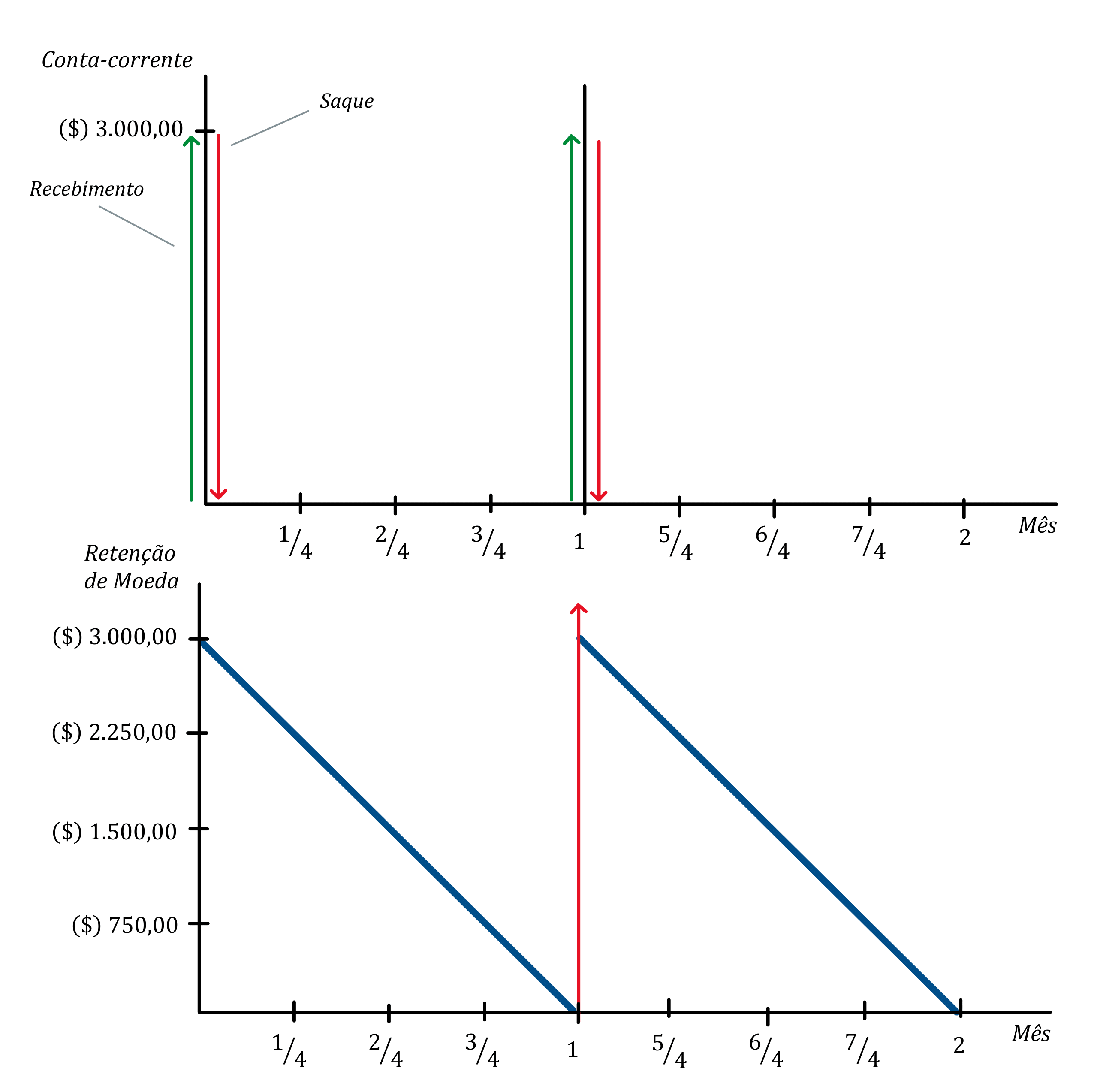
Dessa forma, assim que há o recebimento da renda salarial mensal — deduzindo a poupança e a alíquota de imposto de renda —, o indivíduo representativo vai ao caixa eletrônico e saca a quantia de $ 3.000,00 da renda salarial líquida para o seu consumo mensal. Ou seja, o saldo em conta-corrente no gráfico superior é zerado, e a retenção de moeda (encaixe) no gráfico inferior passa a ser de $ 3.000,00. Dessa forma, devido ao comportamento de consumo contínuo do indivíduo representativo, a retenção de moeda (encaixe) reduz de maneira uniforme ao longo do mês.
Dado a hipótese de comportamento de consumo do indivíduo representativo, é possível calcular a Retenção Média de Moeda (RMM) — ou o Encaixe Médio (EM) — no período mensal considerado a partir da seguinte fórmula:
em que: RMM: Retenção Média de Moeda; RM: Retenção de Moeda; n: Número de transações econômicas.
A intuição dessa fórmula é que o mês é normalizado para a unidade e somado a razão de 1/n, que representa o efeito da quantidade de transações econômicas realizadas (n) para o consumosobre a Retenção Média de Moeda (RMM). Dessa forma, como o comportamento de consumo do indivíduo representativo é uniforme e contínuo, então a RMM é calculada quando n tende ao infinito.
Graficamente, temos:
A partir desse resultado, podemos encontrar a constante marshalliana (k), que é o parâmetro da função de demanda por moeda na visão clássica. Para isso, basta colocarmos o valor da Retenção Média de Moeda (RMM) em razão da renda salarial mensal— ou seja, antes de ser deduzida a poupança e o imposto de renda — recebida pelo indivíduo representativo, que é de $ 5.000,00. Ou seja:
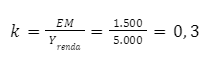
Se o comportamento de consumo do indivíduo representativo puder ser generalizado para a economia como um todo, então podemos considerar que:
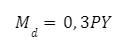
No entanto, percebam que esta função não depende da taxa de juros. Dessa forma, se adotarmos essa função de demanda por moeda para a dedução da curva LM, o seu resultado implica que a curva de demanda por moeda é vertical, podendo ou não coincidir com a curva (vertical) de oferta de moeda. Sendo assim, tomando (k) como rígido no curto-prazo, a demanda por moeda só é influenciada por variações no nível de renda e nível de preços. Isso implica numa curva LM totalmente vertical.
Desse modo, variações na oferta de moeda, apesar de não afetarem as decisões de motivo transação, afetam o preço dos títulos no mercado financeiro, ampliando ou reduzindo o nível de investimento da economia.
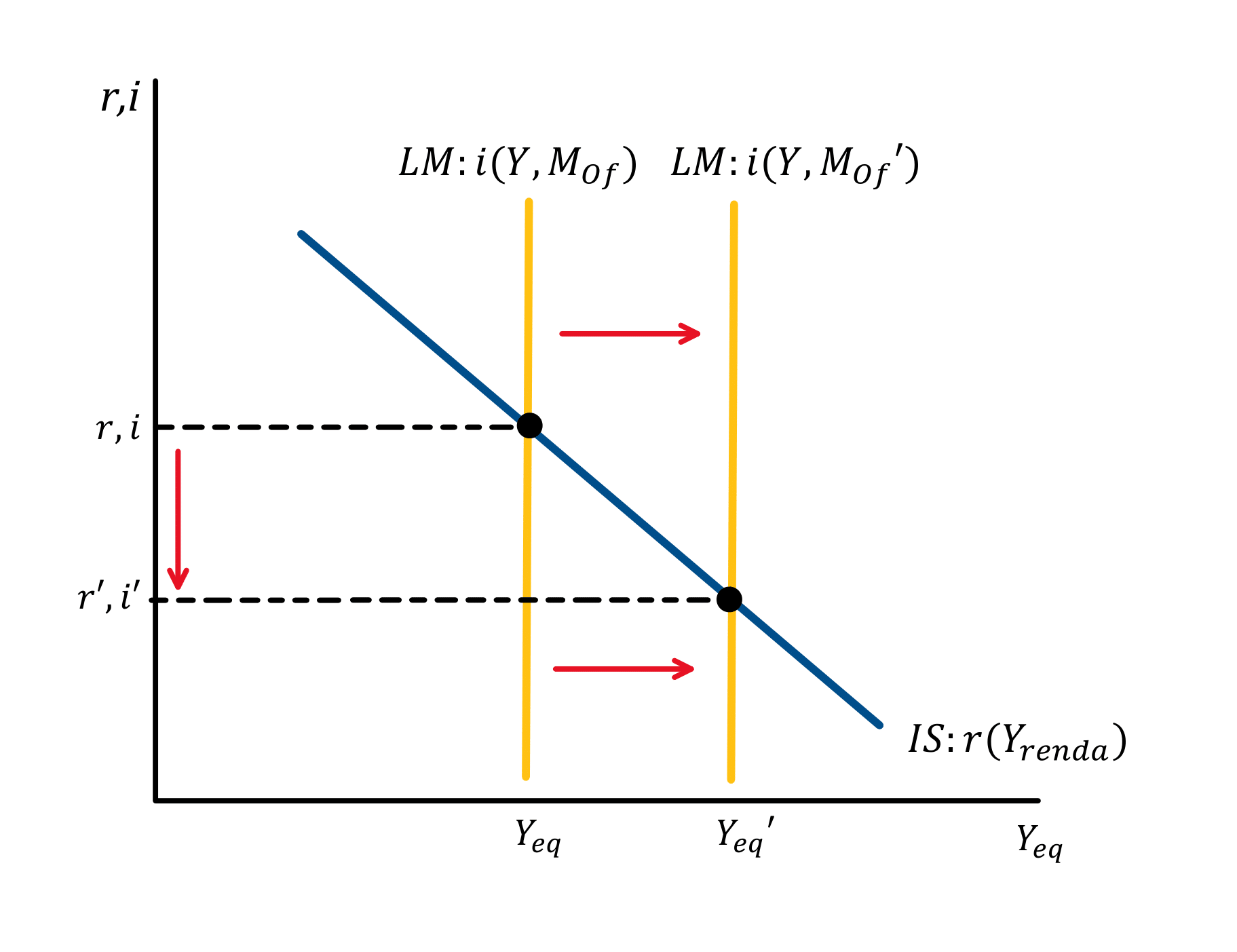
Dessa forma, para introduzirmos a influência da taxa de juros (r) na função de demanda por moeda, é necessário ampliar a abordagem acima. Isso é feito pelo modelo keynesiano Tobin-Baumol de demanda por moeda para o motivo transação.
3.2. O motivo transação — A visão keynesiana, ou o modelo Tobin-Baumol
Conforme exposto anteriormente, a partir da visão clássica, a taxa de juros (r) não exerce influência sobre a demanda de moeda pelo motivo transação. Isso ocorre pois as famílias — representadas pelo comportamento do indivíduo representativo — não possuem acesso a rendimentos financeiros de curto-prazo, ou seja, títulos capitalizados a juros simples e com vencimentos em prazos inferiores a 30 dias. Além disso, apenas a moeda física é considerada como meio de pagamento, o que justifica o comportamento de zerar o saldo em conta-corrente logo após o recebimento da renda salarial mensal, minimizando o inconveniente de ter que ir ao caixa eletrônico para realizar o saque de moeda física.
Dessa forma, sem acesso a rendimentos financeiros de curto-prazo, não há incentivos econômicos para a administração racional dos saldos monetários ociosos. Ou seja, a parte dos saldos monetários que poderiam ser aplicados em títulos, aumentando a liquidez do sistema financeiro, estão retidos pelas famílias.
3.2.1. A oferta de liquidez (ou a demanda de títulos)
O modelo Tobin-Baumol permite a existência de meios de pagamento alternativos,como o cartão de débito, e considera a possibilidade de que as famílias possam aplicar parte da retenção de moeda em títulos de curto-prazo. Desse modo, criam-se os incentivos econômicos necessários para a administração racional da Retenção Média de Moeda (RMM), que deve ser minimizada para maximizar os ganhos com rendimentos em títulos de curto-prazo.
Ou seja, para o exemplo anterior, no primeiro dia do mês, ao invés do indivíduo representativo sacar o total de $ 3.000,00 da renda disponível em conta-corrente, ele faz a retirada de apenas $ 1.500,00, podendo alocar a outra parte ($ 1.500,00) em títulos, que renderão juros até a metade do mês. Chegando na metade do mês, o indivíduo representativo retira os $ 1.500,00 alocados anteriormente em títulos e saca esse mesmo valor da sua conta-corrente para que seja consumido durante a segunda metade do mês. Para fins de simplificação, podemos supor que os juros provenientes dos títulos serão guardados para serem gastos no longo-prazo.
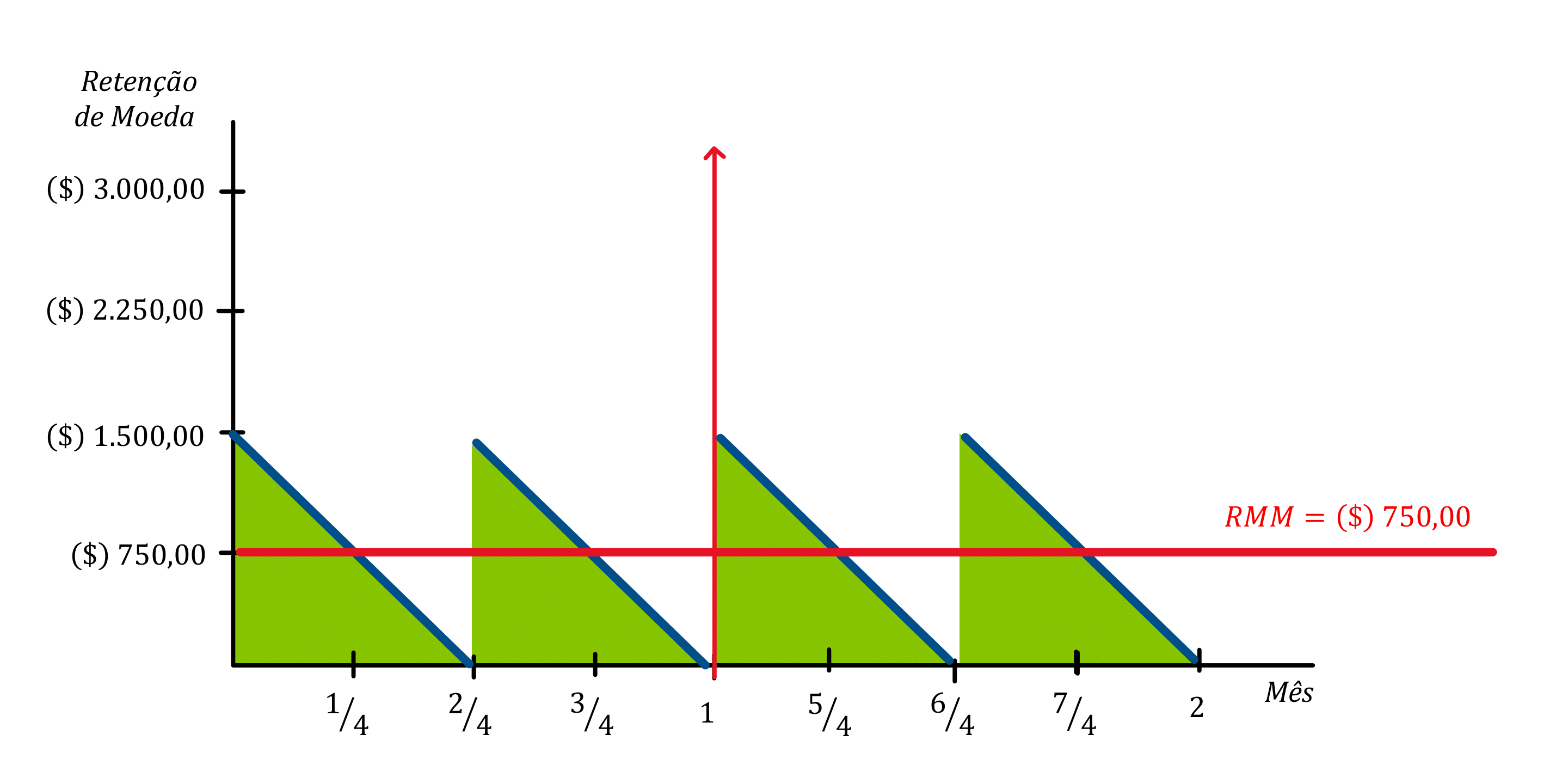
Apesar do indivíduo representativo ter administrado racionalmente a Retenção Média de Moeda (RMM), isso não significa que a RMM tenha sido zerada. Na realidade, ela apenas foi reduzida, e o seu valor passou a ser de $ 750,00.
A intuição por trás disso é bem simples. Dada a relação de proporcionalidade existente, se calcularmos a RMM para a primeira metade do período, então temos a RMM para o período total. A única diferença é que, ao invés de utilizarmos a renda disponível (Y_{disp}) — da forma como foi abordado na seção anterior —, usaremos o volume por retirada (W). Isso faz sentido, haja visto que a Retenção Média de Moeda (RMM) é calculada em função da posse de moeda no período.
Dessa forma, para duas retiradas (N) de mesmo montante, o que equivale a W = 1.500,00, temos:
Para três retiradas (N) de mesmo montante, o que equivale a W = 1.000,00, temos:
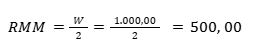
Percebam que podemos estabelecer uma relação entre a renda disponível (Y) e o volume por retirada (W), através da quantidade de retiradas (N). Sendo assim, o volume por retiradas (W) pode ser determinado da seguinte maneira:
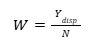
Se substituirmos o W na fórmula da RMM por volume de retirada, temos o seguinte resultado:
em que: RMM: Retenção Média de Moeda; Y_{disp}: Renda disponível; N: Número de retiradas de mesmo montante.
Entender a dedução dessa fórmula para o cálculo da RMM — em função da quantidade de retiradas (N), gerando o mesmo volume por retirada (W) — é importante, pois é a partir dela que o modelo Tobin-Baumol é construído.
Devido à relação de dualidade existente nos problemas de otimização, há duas perspectivas possíveis para a construção do modelo Tobin-Baumol. A primeira perspectiva é a minimização de uma função de Custo (C) de retenção de moeda. A ideia por trás é que, ao reter moeda, o indivíduo representativo deixa de obter o juro referente à quantidade não alocada em títulos. A segunda perspectiva é a maximização de uma função de Lucro (\pi) dos rendimentos em títulos de curto-prazo. A ideia é alocar a maior quantidade possível de moeda em títulos de curto-prazo.
Apresentaremos as duas formas, começando pela minimização de Custo Total (CT) e depois pela maximização do Lucro (\pi).
Apesar de pouco intuitiva, a minimização do Custo Total (CT) de retenção de moeda é a abordagem padrão de livro-texto para a construção do problema do modelo Tobin-Baumol. A otimização se dá através da redução da Retenção Média de Moeda (RMM) para o seu valor ótimo, utilizando a quantidade de retiradas “N” como variável de controle, mas que também está sujeita ao custo de corretagem “c” por cada retirada.
O problema é dado da seguinte maneira:
em que: i: Taxa de juros mensal; Y_{disp}: Renda disponível; N: Quantidade de retiradas de mesmo valor; c: Custo por retirada.
O primeiro termo do lado direito da equação representa o juro perdido por não realizar a retirada (representa, portanto, um custo de oportunidade). Dessa forma, se a renda disponível do indivíduo representativo é de $ 3.000,00, então ao realizar 2 retiradas, a RMM está em $ 750,00; se a taxa de juros mensal (i) é 0,04, então o indivíduo representativo deixa de ganhar $ 30,00 de juros.
Por conseguinte, ao realizar 3 retiradas de mesmo valor, o indivíduo deixa de ganhar $ 20,00 de juro. O juro perdido somado ao custo agregado de todas as retiradas, cN, representa a função de Custo Total (CT), que precisa ser minimizada.
Derivando a função CT em relação a N, encontramos a condição de primeira ordem:
Resolvendo para a quantidade de partições de renda disponível, N, temos a quantidade de partições que minimiza a função de Custo Total (CT) de retenção de moeda:
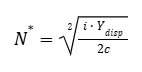
Graficamente, o problema é representado da seguinte maneira:
Outra forma de montar o problema do modelo Tobin-Baumol — que é mais intuitiva — envolve a criação de um problema de maximização do rendimento obtido com a alocação do saldo em conta-corrente em títulos de curto-prazo. A intuição é que podemos abordar o problema de outro ângulo, ou seja, tratando a quantidade alocada em títulos de curto-prazo como resíduo da RMM. Dessa forma, conforme a quantidade de retiradas “N” aumenta, então a RMM diminui, aumentando a Retenção Média de Títulos (RMT).
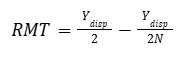
Dessa forma, acrescentando a existência de um custo de corretagem “c” por cada “N-1” quantidade de retiradas de mesmo valor — esse “-1” é necessário pois a primeira retirada do período não possui custo de corretagem —, o problema fica da seguinte maneira.
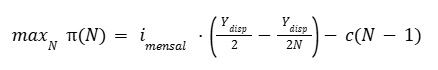
em que: i: Taxa de juros mensal; Y_{disp}: Renda disponível; N: Quantidade de retiradas de mesmo valor; c: Custo por retirada.
Derivando a função em relação a N, encontramos a seguinte condição de primeira ordem:
Resolvendo para o a quantidade de retiradas (N), temos a quantidade de retiradas que maximiza a função de rendimento (\pi) de retenção média de títulos (RMT):
Podemos perceber que a quantidade de retiradas ótima (N*) que maximiza a função de rendimento é a mesma que minimiza a função de custo total de retenção de moeda.
Graficamente, o problema é representado da seguinte maneira:
Dessa forma, a quantidade de retiradas N que maximiza o rendimento é a que torna a inclinação da curva de rendimento total (RT), em azul, igual a inclinação da curva de custo (C), em vermelho.
3.2.2 A oferta de títulos (ou a demanda por liquidez)
Uma forma de incorporar o N ótimo para deduzir uma função de demanda por moeda é supor que , pelo menos num caso mais simples , enquanto metade da economia está aplicando uma parte da RMM — análogo a estar ofertando liquidez para o sistema financeiro —, necessariamente a outra metade está demandando essa mesma quantidade em liquidez — análogo a estar ofertando títulos de curto-prazo.
Por exemplo, os Bancos Comerciais (BACOMs) podem oferecer títulos de curto-prazo para obter a liquidez das famílias. Com esses recursos, dada a existência de economias de escala em operações bancárias, os BACOMs podem utilizar os recursos obtidos para operações de empréstimos de prazos mais longos.
Sendo assim, para esse caso, podemos interpretar a equação da RMM de maneira invertida, ou seja, como sendo uma função de demanda por moeda dos Bancos Comerciais, em que “n” é a quantidade de capitalizações que iguala exatamente ao número de retiradas “N” da renda disponível das famílias.
Substituindo para o N ótimo (N*) encontrado nos problemas de otimização colocados acima, temos:
onde M_d é a demanda por moeda (liquidez) dos Bancos Comerciais, que é exatamente igual a RMM.
Se considerarmos que:
temos, a seguinte função de demanda por moeda por motivo transação derivada do modelo Tobin-Baumol:
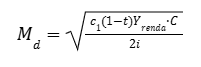
Resolvendo a função de demanda por moeda acima para a taxa de juros (i), temos:
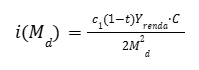
Considerando que a oferta de moeda (M_{of}) é exógena, e que no modelo IS-LM não se leva em conta a inflação, de modo que a taxa de juro real (r) é igual a taxa de juro nominal (i), então temos o seguinte gráfico:
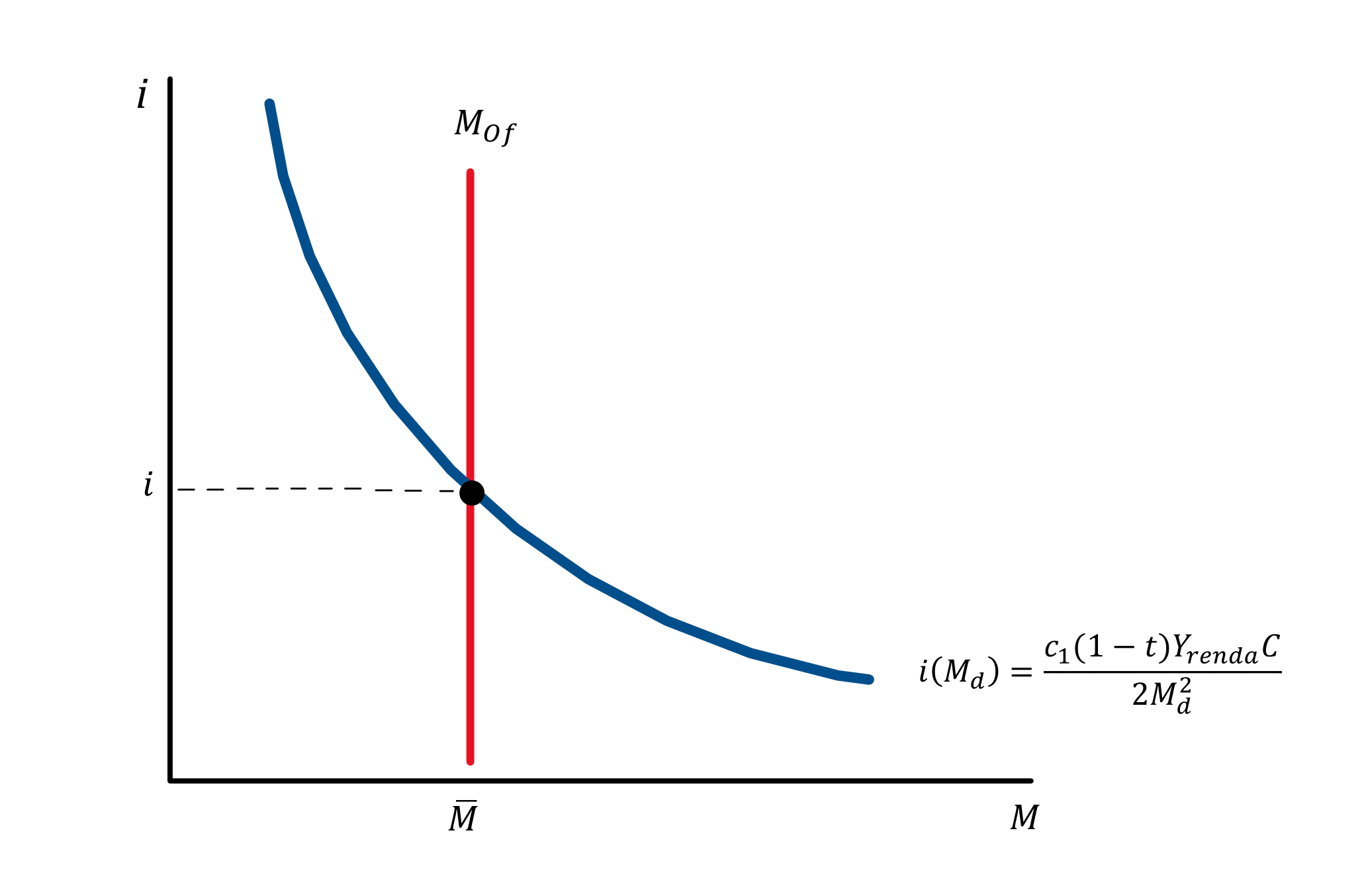
Sendo assim, para deduzir a curva LM, basta colocar a renda (Y) como argumento da função de demanda por moeda:
O resultado gráfico é semelhante ao caso anteriormente deduzido:
4. O modelo IS-LM completamente deduzido
Agora que deduzimos o equilíbrio no mercado monetário/financeiro e a curva LM através do modelo Tobin-Baumol de demanda de moeda, podemos encontrar o equilíbrio simultâneo com o mercado de bens, através da interação da curva IS com a LM. Desse modo, resolvendo o modelo, temos o produto e a taxa de juros de equilíbrio da economia.
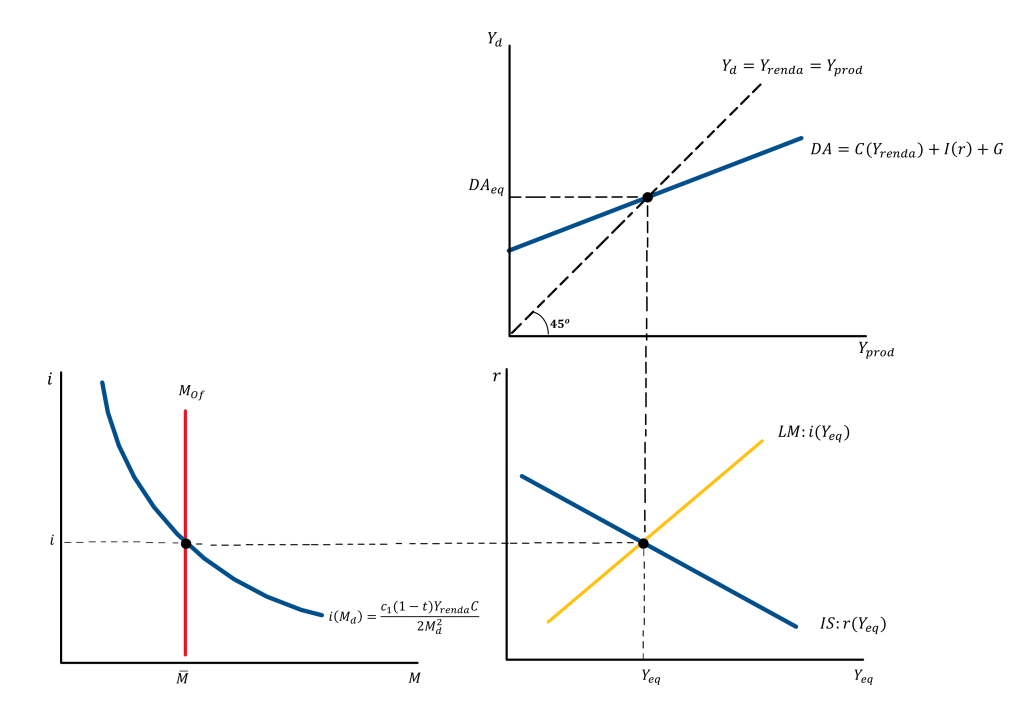
E a solução de equilíbrio do modelo é quando a função que descreve a curva IS se iguala à função que descreve a curva LM:
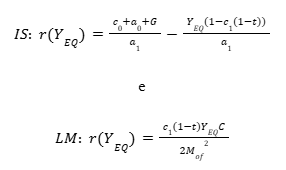
Ou seja, o equilíbrio ocorre quando:
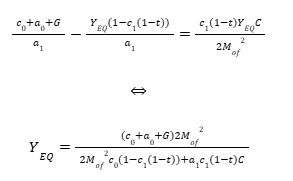
Para encontrar a taxa de juros, basta substituir o produto de equilíbrio na IS ou LM. Substituindo na LM:
A intuição básica desse modelo é que a autoridade monetária, ao manipular a oferta de moeda, altera o custo de oportunidade dos Bancos Comerciais (BACOMs) para a oferta de novos títulos de curto-prazo. Sendo assim, para um aumento da oferta de moeda, a maior liquidez do sistema financeiro incentiva os BACOMs a reduzirem a taxa de juros (i) em novos títulos emitidos. No modelo Tobin-Baumol, isso significa uma redução da quantidade N de inversões e um aumento da Retenção Média de Moeda (RMM) das famílias representadas pelo indivíduo representativo.
De forma análoga, para uma redução da oferta de moeda, a menor liquidez do sistema financeiro incentiva os BACOMs a aumentarem a taxa de juros (i) em novos títulos emitidos. No modelo Tobin-Baumol, isso significa um aumento da quantidade N de inversões e uma redução da Retenção Média de Moeda (RMM) das famílias representadas pelo indivíduo representativo.
Referências
LOPES, Luiz Martins (Org.) et al. Manual de Macroeconomia: Nível Básico e Nível Intermediário. 3 ed. São Paulo: Atlas S.A, 2008.
Deixe um comentário