A macroeconomia é uma área de estudo da Ciência Econômica que busca compreender o funcionamento — e as relações — entre variáveis econômicas agregadas, de modo a compreender os efeitos econômicos, principalmente sobre o produto da economia, dada uma mudança em alguma das variáveis consideradas. No entanto, a própria macroeconomia é subdividida em três grandes subgrupos, e cada grupo trata de um problema específico a ser analisado. A diferença de cada subgrupo se dá em função de um aspecto temporal: o curto-prazo, o médio-prazo e o longo-prazo. Devemos lembrar que o tempo em matéria de economia na graduação é um conceito próprio da disciplina.
Para entender isso de forma mais fácil, vamos nos lembrar das aulas de microeconomia. Os agentes econômicos otimizam suas escolhas de modo a gerar uma maior quantidade de bem-estar (para famílias) e lucro (para as firmas), dada uma certa restrição econômica. Desse modo, como estamos lidando principalmente com aspectos de produção, a intuição é que as firmas escolhem uma combinação de insumos produtivos que maximizam o lucro — ou, de modo análogo, minimizam os custos.
Dessa maneira, podemos partir da hipótese de que o Produto (Y) é o fator resultante da associação entre dois insumos produtivos: Capital (K) e Trabalho (L). Matematicamente:
Sendo assim, adicionamos outro pressuposto — bem razoável — de que, no curto-prazo, a produção (Y) se modifica variando o fator Trabalho (L) e mantendo o nível de capital (K) fixo. Já, no longo prazo, tanto Capital (K) quanto Trabalho (L) podem variar para alterar o nível de produção.
A teoria macroeconômica segue, em parte, essa lógica temporal. No curto-prazo, apenas o fator Trabalho (L) é alterado. Ou seja, caso haja choques exógenos na economia, o consumo será alterado e, portanto, a produção precisa se adequar. As firmas modificam o nível de fator Trabalho (L) empregado no processo produtivo buscando maximizar o lucro, o que acaba por alterar novamente o nível de consumo. Esse ciclo se repete até que o novo equilíbrio seja atingido.
O médio prazo é um conceito mais circunscrito da macroeconomia, que analisa o processo de reajuste de preços e o retorno ao equilíbrio geral da economia. O equilíbrio geral representa o fim último da política econômica de curto-prazo e é determinado por parâmetros estruturais da economia.
Já no longo prazo, se estuda os determinantes do crescimento econômico, dado que tanto Capital (K) quanto Trabalho (L) podem variar e alterar o nível de produção.
De outra forma, o ponto fundamental da macroeconomia de longo-prazo é entender como os fatores de produção evoluem, e agora, necessariamente, em como os fatores de produção evoluem no tempo de ordem cronológica.
Se Capital (K) e Trabalho (L) evoluem no tempo, então o Produto (Y) também evolui no tempo. No entanto, como nossa análise busca entender precisamente o crescimento econômico, precisamos especificar nossa função de produção em termos per capita. No caso, para efeitos didáticos, vamos assumir que toda a população está empregada. Desse modo, o produto per capita é:
Essa especificação é necessária, pois — dependendo de como os insumos são transformados em Produto (Y) — é possível que, com o aumento da produção ao aumentar o fator trabalho, o produto per capita se reduza. Ou seja, a renda total por habitante é menor que antes. Isso ocorre devido à hipótese de rendimentos marginais decrescentes dos fatores de produção, que será melhor explicada mais à frente.
2. Introdução ao Modelo de Solow
Até o momento, fizemos uma breve contextualização a respeito do objeto de estudo da Macroeconomia de longo-prazo — ou seja, o crescimento econômico. Entendemos que o produto da economia é determinado por uma associação entre insumos produtivos: Capital (K) e Trabalho (L), de modo que, se esses insumos produtivos variam no tempo (t), o produto também varia no tempo (Y(t)). No entanto, o foco da análise não é apenas variação do produto total, mas a variação do produto per capita (Y(t)/L(t)), pois este sim é o determinante do crescimento econômico e do aumento de bem-estar social.
Em geral, o primeiro modelo de crescimento econômico estudado nos cursos de Macroeconomia é o Modelo de Solow. Como o próprio nome diz, ele foi desenvolvido por Robert M. Solow, que publicou, em 1956, o artigo seminal “A Contribution to The Theory of Economic Growth”. Apesar de ser um artigo muito interessante e extremamente didático, a notação usada por Solow é um pouco diferente da utilizada pelos manuais atuais. Mas a estrutura básica é mais ou menos a mesma, sendo ela composta por quatro equações fundamentais, que são as seguintes:
1. O produto total de uma economia fechada, sem governo e em competição perfeita:
2. Uma função de produção bem-comportada, especificada em termos per capita:
3. Uma função de crescimento populacional padrão:
4. A equação da dinâmica de acumulação de Capital (K):
A partir dessas quatro equações, iremos construir nosso modelo. Mas antes, para que essas relações façam sentido, precisamos explorar com mais cuidado o significado econômico por trás de cada uma delas.
3. A economia fechada, sem governo e perfeitamente competitiva
Apesar de ser uma simplificação extrema, esse ponto de partida tem como objetivo facilitar a nossa análise, para que a intuição econômica por trás do modelo seja adquirida de forma mais rápida. A partir dessa suposição, podemos concluir, por exemplo, que a função de produção dessa economia precisa ser bem-comportada e com retornos constantes de escala — o que será abordado mais a frente. Dado isso, podemos estabelecer relações entre as identidades estudadas em Contabilidade Nacional.
Se a economia é perfeitamente competitiva, então temos que a oferta sempre será igual à demanda. Portanto, o produto total da economia será equivalente à sua renda total. Isso significa que os rendimentos gerados durante o processo produtivo são suficientes para financiar a sua produção. Ou seja, a Lei de Say é satisfeita. Desse modo, se a produção é igual a renda, e estamos modelando uma economia fechada e sem governo, a seguinte propriedade é verdadeira:
O volume de Investimento (I) é igual à Poupança (S). Essa igualdade será importante para entender a equação da dinâmica de acumulação de Capital (K).
4. A função de produção bem-comportada
Como dito anteriormente, a função de produção representa uma associação entre insumos produtivos (K, L) que resultam numa determinada quantidade de bens produzidos (Y). Isso, no entanto, não é suficiente para que a função de produção tenha sentido econômico. Essa função precisa ser acompanhada de alguns pressupostos adicionais. Esses pressupostos são bem razoáveis e, caso necessário, podem ser flexibilizados.
A primeira suposição é de que, ao variar um fator de produção, e mantendo o outro fator constante, o produto aumenta em taxas decrescentes. Ou seja, o produto marginal do fator de produção é decrescente. Matematicamente, isso significa que a primeira derivada parcial em relação ao fator de produção é positiva, e a segunda derivada é negativa. Essa condição deve ser satisfeita tanto para o Capital (K) quanto para o Trabalho (L), e o comportamento deve ser consistente ao longo de toda a curva. Analiticamente:
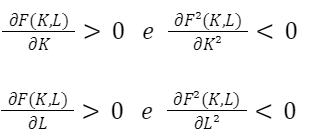
Graficamente, temos:
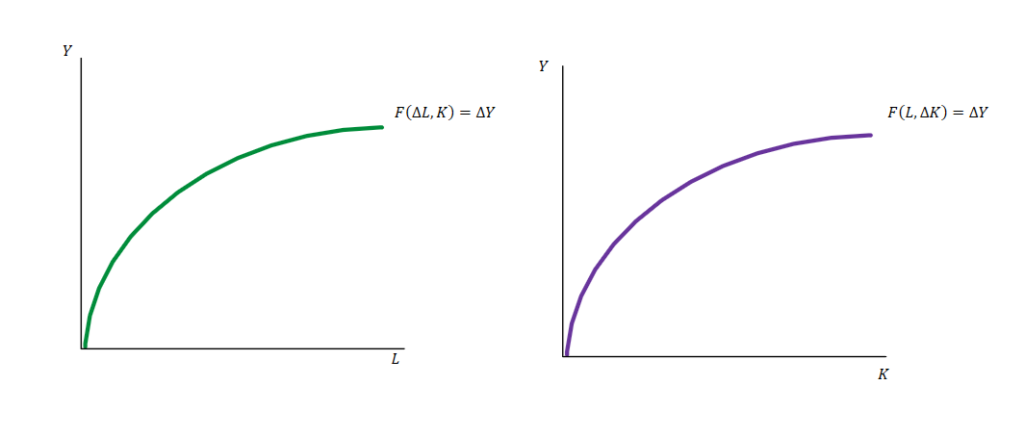
Outra condição que utilizaremos é a de que a função de produção precisa exibir retornos constantes de escala. Ou seja, ela precisa ser homogênea de grau 1, respeitando a seguinte transformação monotônica:
Isso significa que se dobrarmos a quantidade de Capital (K) e Trabalho (L), o produto (Y) também irá dobrar. A implicação dessa suposição é de que a nossa economia modelada é altamente especializada e composta por milhares de pequenas firmas. Sendo assim, estamos diante de uma economia de competição perfeita, garantindo a conclusão anterior.
Graficamente:
Quando a função de produção exibe o formato acima, dizemos que ela é bem comportada, o que implica em simular uma economia perfeitamente competitiva.
Existe uma função que a sua forma funcional satisfaz todas as condições acima: a função Cobb-Douglas. Utilizaremos ela para simular a produção da nossa economia.
Se assumirmos que toda a população está empregada, então o produto per capita dessa função é:
Graficamente, a função de produção acima exibe o mesmo comportamento que a anterior. Ou seja:
Agora que sabemos como o produto per capita da nossa economia é determinado, vamos entender como os insumos produtivos evoluem no tempo.
5. Como Trabalho (L) e Capital (K) evoluem no tempo?
Como estamos tratando a respeito de crescimento econômico, nosso objetivo é entender o que acontece com o produto per capita da economia quando a variação de Capital (K) e Trabalho (L) no tempo é determinada — cada uma — por uma função específica. Ou seja:
5.1. Crescimento do fator Trabalho (L)
Dado que na nossa economia toda a população está empregada, podemos modelar o crescimento do fator Trabalho (L) de maneira análoga ao modelo de crescimento populacional malthusiano. Desse modo, vamos partir da hipótese de que a população (L) cresce em função do tempo (t) a uma taxa (n) proporcional ao seu tamanho (L). Ou seja, a sua derivada exibe o seguinte comportamento:
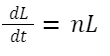
Se isolarmos os termos para L, encontramos:
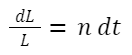
Temos uma função de derivada total que representa a taxa de crescimento populacional no tempo. Agora queremos encontrar uma função que resulte no nível populacional no tempo. Ou seja, precisamos resolver a Equação Diferencial acima, encontrando a sua antiderivada (ou primitiva).
Dado a propriedade dos exponenciais, e considerando que L > 0, temos:
Sendo assim, se atribuirmos t = 0 na função acima, encontramos o nível da população inicial:
Podemos então substituir o resultado por L_0 para obter a função populacional final:
5.2. Crescimento do fator Capital (K)
Já sabemos como o fator Trabalho (L) evolui, agora precisamos saber como se dá a dinâmica do Capital (K). É intuitivo pensar que a variação de Capital (K) depende do fluxo de Investimento (I) menos a depreciação do Capital (K). Ou seja:
em que \delta representa a taxa pela qual o Capital no período foi depreciado.
Para elaborar melhor o nosso modelo de crescimento do Capital (K), precisamos especificar a origem do Investimento (I). Sabemos que o volume de Investimento (I) da nossa economia é igual ao seu volume de Poupança (S):
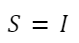
Se assumirmos que a Poupança da economia é proporcional à renda total, então temos que:
Portanto:
Para efeitos simplificativos, não iremos deduzir a primitiva da equação diferencial acima. O formato acima é suficiente para montarmos o modelo básico de Solow.
6. Montando o Modelo de Solow
6.1. Deduzindo a equação fundamental do modelo
Como estamos lidando com variáveis per capita, então podemos escrever:
A diferencial total da equação acima é:
Simplificando as variáveis per capita, temos:
Sabemos que o produto per capita é uma função de capital per capita. Logo:
Equação (1)
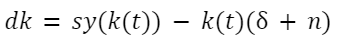
A equação acima é denominada Equação Fundamental de Solow. O termo do lado esquerdo (dk) expressa a variação líquida do capital per capita. O primeiro termo do lado direito [sy(k(t))] expressa a variação bruta do capital, ou seja, o volume de Investimento per capita no tempo (t). O segundo termo do lado direito representa a proporção (\delta) do capital per capita depreciado junto com a sua redução dado o crescimento populacional (n).
Essa equação nos mostra que, quando a variação do capital per capita (dk) é igual a zero, então temos a seguinte igualdade:
Isso significa que a economia não está crescendo em termos per capita. Portanto, estamos no estado estacionário da economia.
6.2. A representação gráfica do modelo
A representação gráfica do modelo pode ser feita atribuindo a cada termo da equação (1) uma função própria. Desse modo:
Esse diagrama é denominado Diagrama de Solow. Num primeiro momento, a intuição econômica dele é difícil de perceber. Mas, se especificarmos cada variável, a intuição se torna facilitada.
O ponto crucial para entender a curva acima é que, conforme vimos anteriormente, o capital per capita varia em função do Capital Agregado (K) e do Trabalho Agregado (L). O caso especificado pela curva é quando apenas o Capital Agregado (K) está variando. Nesse caso, quando colocamos na função de produção, temos o seguinte:
Mas apenas a proporção s é destinada ao Investimento (I) da economia. E é por isso que a função exibe o formato côncavo.
Mas e a variação do capital per capita induzida pela taxa depreciação (\delta) e pela taxa de crescimento populacional (n)? Esse efeito é captado pela segunda função do diagrama de Solow:
A intuição por trás desse gráfico é que um aumento proporcional de Trabalho (L) pode ser entendido como uma redução relativa de Capital (K). Assim sendo, uma redução proporcional de Capital (K) pode ser entendida como um aumento relativo de Trabalho (L).
A interação entre essas duas funções nos gera o valor do capital per capita (k), segundo o qual o produto marginal do Investimento (I) é igual a redução do produto per capita dada pela taxa de depreciação e pela taxa de crescimento populacional. Isso significa que, apesar do produto total aumentar, o produto per capita da economia permanece constante.
Desse modo, concluímos o objetivo do nosso texto. Entendemos o objeto de estudo da Macroeconomia do Crescimento Econômico, bem como o motivo de avaliarmos o crescimento per capita, e deduzimos o Modelo de Solow. Outro ponto importante é entender o que acontece com o modelo quando alteramos, por exemplo, a taxa de poupança (s) da economia e o efeito disso sobre o consumo per capita. Mas isso precisa de um texto específico.
Referências
Ramos, C. A. Nota didática 3: O Modelo de Solow.
Romer, D. (2011). Advanced Macroeconomics. McGraw-Hill, Fourth Edition.
Charles, Jones. Introdução à Teoria do Crescimento Econômico.
Deixe um comentário