O primeiro contato com a microeconomia intermediária do graduando é simples e serve ao propósito de aprender o conteúdo do livro-texto, talvez até passar em uma prova como a ANPEC. Entretanto, essa exposição carece de profundidades do dia-a-dia incorporadas em modelos mais sofisticados, que são factíveis de serem aprendidos pelos alunos, mas cuja chance lhes é roubado em prol de seguir um roteiro definido. Sendo assim, o aluno fica com a impressão que a teoria do consumidor é apenas uma abstração inútil e descolada da realidade, Mas nada esta mais distante da verdade. Para demonstrar isso, apresentarei o modelo da função de produção familiar desenvolvido pelo economista Gary S. Becker em seu artigo seminal de 1965 intitulado “A Theory of the Allocation of Time“.
Em primeiro lugar se faz necessário explicar o pano de fundo enfrentado pelo aluno: a construção de uma teoria da demanda (leia mais sobre neste texto) consistente e completa tem sido uma grande fonte de orgulho para os economistas, dado a vasta gama de fenômenos que podem ser explicados por esta e suas mais variadas aplicações. Um exemplo de bate-pronto de aplicação é a teoria dos leilões, teoria esta que rende bilhões para a Google com adsense (mais pode ser lido neste texto). Entretanto, a rica complexidade e nuances dessa teoria passa despercebido ao aluno de graduação que tem contato apenas com os modelos mais simples de teoria da escolha (no caso são o modelo de decisão sob certeza e decisão sob incerteza do tipo Von Neumann-Morgenstern).
A ideia geral do que é ensinado sobre teoria do consumidor se desvincula de qualquer conversa sobre produção. Apenas são escolhidos os bens pelos indivíduos e raramente é dito que a quantidade escolhida é uma taxa, assim questões temporais passam a ser ignoradas, sendo apenas mencionadas na parte de escolha intertemporal com dois períodos.
Daí entra-se em teoria de produção e um novo mundo é introduzido. Neste novo campo (para saber mais sobre recomendo a leitura deste texto), a explicação é feita de tal modo que parece ignorar toda a parte que veio anteriormente. Como se o indivíduo, que era representado com um problema de otimização restrita, agora se torna apenas um elemento da variável representada pelo L na função de produção. Tudo isso com a promessa de que quando chegar em equilíbrio geral tudo irá se conectar.
Talvez um estudante mais perspicaz se leve a perguntar: por que quando a renda de um indivíduo aumenta a qualidade dos bens que ele consome também aumenta? Ou seja, porque o indivíduo substitui seu consumo para bens de qualidade maior quando sua renda aumenta ao invés de comprar as mesmas coisas?
Talvez isso decorra do fato de que o indivíduo consome apenas bens inferiores, i.e., bens cujo consumo diminui quando a renda do indivíduo aumenta (para saber mais recomendo este texto). Mas ainda assim é resultado desconfortável, afinal não pode ser o caso que todos os seus bens consumidos sejam inferiores e não parece satisfatório dar uma resposta via preferências. Se um bem é normal, então o modelo padrão nos prevê que o indivíduo simplesmente iria consumir mais dos bens que já consome sem se importar com sua qualidade. Como resolver isso?
Seria uma limitação dos seus desejos? Ou resultado de alguma restrição? Na realidade, o problema é mais profundo. Sem precisar recorrer as respostas ad hoc, i.e., respostas que não partem de primitivos do modelo e que geralmente não são condizentes com o modelo original e são apenas utilizados para fazer o modelo se ajustar aos dados, a dificuldade de prover uma resposta vem da ilusão promovida pelo jeito que montamos o problema do consumidor. É a ilusão de que a teoria da demanda de alguma maneira está embutida na mente das pessoas, ou seja, como se por trás da teoria da demanda houvesse uma teoria psicológica ingênua implícita. Entretanto, a maioria do que sabemos dessa teoria se aplica para além das pessoas, advindo das decisões observadas destas e do processo produtivo pelo qual construímos o que no fim consumimos.
O que está em jogo aqui é que a separação rígida entre produção e consumo é indevida, embora útil por motivos pragmáticos em algumas situações. As pessoas não meramente consomem bens isolados, mas sim bens compostos que advêm de um processo produtivo. Um exemplo é o teatro, pois ir ao teatro não só envolve uma combinação de bens (transporte, ingresso, alimentos, etc.), como também envolve tempo. Dado que esse tempo é recurso escasso, então existem custos indiretos no consumo do teatro, na medida em que o tempo gasto para ir ao teatro poderia estar sendo consumido de maneira produtiva. Ou seja, há um custo de oportunidade.
Então a resposta à pergunta acima (“por que quando a renda de um indivíduo aumenta a qualidade dos bens que ele consome também aumenta?“) fica mais evidente com um exemplo: com uma dada renda, faço uma viagem para a praia de Ipanema dados meus custos e benefícios. Assim que minha renda aumenta e os custos associados ao uso do meu tempo também, ao invés de fazer doze viagens para Ipanema, faço uma viagem para Ibiza.
Esse exemplo se baseia na resposta que Gary Becker deu ao problema em seu célebre paper de 1965. Para entender melhor a reposta, é preciso adentrar no modelo econômico proposto pelo autor. Portanto, é disso que nos ocuparemos agora.
Modelo da função de produção familiar
A exposição a seguir é essencialmente uma tradução do artigo original de Becker, uma vez que a exposição é clara o suficiente para qualquer um entender. Entretanto, focaremos apenas nas partes que dizem respeito ao modelo e não suas aplicações (assim, se for do interesse do leitor, recomendo fortemente a leitura do paper). Vamos ao modelo.
De acordo com a teoria da demanda tradicional, os indivíduos maximizam sua função utilidade com a seguinte forma:

Sujeito à seguinte restrição:

Em que yi são os bens comprados no mercado, pi é o vetor de preços desses bens, I é a renda do indivíduo, que pode ser dividida na sua renda advinda do trabalho, W, e a renda advinda de outras fontes, V, quaisquer que sejam. Como discutimos, o ponto de partida aqui é a incorporação sistemática do tempo que não é advindo do trabalho. Presume-se que as famílias combinem tempo e bens de mercado para produzir mercadorias mais básicas que entram diretamente em suas funções de utilidade. Tais mercadorias serão denominadas de Zi e são representadas da seguinte maneira:
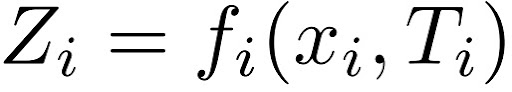
Em que xi é o vetor de bens de mercado e Ti o vetor de insumos de tempo usado para produzir a mercadoria i. Neste modelo, os agentes são tanto produtores de mercadorias quanto maximizadores de utilidade. Combinam seu tempo e os bens de mercado em uma função de produção fi para produzir a mercadoria Zi e escolhem a melhor combinação dessas mercadorias da maneira convencional, maximizando uma função de utilidade:

Sujeito à restrição:

Em que g é a função dispêndio de Zi e Z é o limite dos recursos.
O objetivo básico da análise é encontrar medidas de g e Z que facilitem o desenvolvimento de implicações empíricas. A abordagem mais direta é assumir que a função de utilidade especificada é maximizada sujeita a restrições separadas sobre o gasto de bens de mercado e tempo, e às funções de produção Zi. A restrição de bens pode ser escrita como:
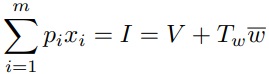
onde pi é um vetor que dá os preços unitários de xi, Tw é um vetor que dá as horas gastas no trabalho e w é um vetor que dá os ganhos por unidade de Tw.
As restrições de tempo podem ser escritas como:

onde Tc é um vetor que dá o tempo total gasto no consumo e T é um vetor que dá o tempo total disponível. As funções de produção podem ser escritas na forma equivalente:
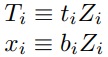
onde ti é um vetor que fornece a entrada de tempo por unidade de Zi e bi é um vetor semelhante para bens de mercado.
Agora, o problema passa a ser meramente maximizar a utilidade descrita com as restrições de forma estendida que estabelecemos acima. Existe, no entanto, apenas uma restrição básica: unificar todas as expressões em uma só, dado que não são independentes umas das outras.

Nisso, podemos expandir a restrição acima de tal modo que fique:
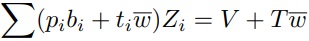
Simplificando, temos:

O preço total de uma unidade de Z_i (\pi_i) é a soma dos preços das mercadorias e do tempo gasto por unidade de Zi. Ou seja, o preço total do consumo é a soma dos preços diretos e indiretos. Esses preços diretos e indiretos são determinantes simétricos do preço total e não há razão analítica para enfatizar um em detrimento do outro.
A restrição de recursos no lado direito da equação da restrição reescrita, S’, é fácil de interpretar se w fosse uma constante, independente de Zi. Pois então S’ dá a renda monetária obtida se todo o tempo disponível fosse dedicado ao trabalho. Essa renda realizável é “gasta” nas mercadorias Zi, seja diretamente por meio de gastos com bens, \Sigma p_i b_i Z_i, ou indiretamente por meio da renúncia de renda, \Sigma t_i w Z_i, ou seja, usando o tempo para consumo em vez de trabalho. Enquanto w fosse constante, e se houvesse retornos constantes na produção de Zi, de modo que bi e ti fossem fixados para dados pi e w, a condição de equilíbrio resultante da maximização assume uma forma muito simples:
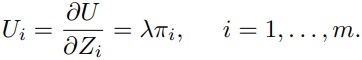
onde \lambda é a utilidade marginal da renda monetária. Se w não fosse constante, a restrição de recursos na equação não teria nenhuma interpretação particularmente útil: S’ = V + Tw exageraria a renda monetária alcançável enquanto os salários marginais estivessem abaixo dos salários médios. Além disso, as condições de equilíbrio se tornariam mais complicadas do que o resultado obtido, pois os preços marginais teriam que substituir os preços médios.
A restrição total de recursos poderia receber a interpretação sensata da renda monetária máxima alcançável apenas no caso especial e improvável em que os rendimentos médios fossem constantes. Isso sugere abandonar a abordagem baseada na consideração explícita de bens separados e restrições de tempo e substituí-la por uma em que a restrição total de recursos seja necessariamente igual à renda monetária máxima alcançável, que será chamada simplesmente de “renda total”. Em geral, essa renda poderia ser obtida dedicando todo o tempo e outros recursos de um domicílio para obter renda, sem levar em conta o consumo. Claro, todo o tempo normalmente não seria gasto “no” trabalho: dormir, comer e até mesmo lazer são necessários para a eficiência, e algum tempo (e outros recursos) teria que ser gasto nessas atividades para maximizar a renda monetária. O valor gasto seria, no entanto, determinado apenas pelo efeito na renda e não por qualquer efeito na utilidade.
Famílias em países mais ricos, no entanto, abrem mão da renda monetária para obter utilidade adicional, ou seja, trocam a renda monetária por uma quantidade maior de renda psíquica. Por exemplo, eles podem aumentar seu tempo de lazer, escolher um emprego agradável em vez de um desagradável com melhor remuneração, empregar sobrinhos improdutivos ou comer mais do que o justificado por considerações de produtividade. Nessas e em outras situações, a quantidade de dinheiro perdido mede o custo de obtenção de utilidade adicional.
Assim, a abordagem de renda total fornece uma restrição de recursos significativa e firmemente baseada no fato de que bens e tempo podem ser combinados em uma única restrição geral porque o tempo pode ser convertido em bens por meio da renda monetária. Também incorpora um tratamento unificado de todas as substituições de rendimentos não pecuniários por pecuniários, independentemente da sua natureza ou se ocorrem no trabalho ou no agregado familiar. As vantagens disso ficarão claras à medida que a análise prosseguir.
Se a renda total for denotada por S, e se o total de ganhos sacrificados ou “perdidos” pelo interesse na utilidade é denotado por L, a identidade relacionando L a S e I é simplesmente:

I e L são funções de Zi porque o quanto se ganha ou se perde depende do conjunto de consumo escolhido; por exemplo, até certo ponto, quanto menos lazer escolhido, maior a renda monetária e menor a quantia perdida.

Vale a nota de que a receita total é obtida maximizando a função de ganhos:

Sujeita à seguinte restrição, representada pela função dispêndio de tempo:
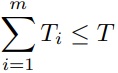
E pelas restrições definindo Ti e xi.
De qualquer modo, a restrição básica de recursos L afirma que a renda total é gasta diretamente em bens de mercado ou indiretamente por meio da renúncia à renda monetária. Infelizmente, não existe uma expressão simples para o preço médio de Zi como na restrição expansiva que tínhamos derivado. No entanto, os preços marginais, e não médios, são relevantes para o comportamento, e seriam idênticos para aquela restrição apenas quando os rendimentos médios, w, fossem constantes. Mas, se assim for, a expressão para a função de perda é simplificada para:
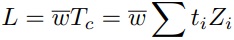
e S reduz a restrição expansiva.
Além disso, mesmo no caso geral, os preços marginais totais resultantes de S podem sempre ser divididos em componentes diretos e indiretos: as condições de equilíbrio resultantes da maximização da função de utilidade sujeita a S são:
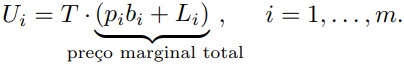
onde pibi é o componente direto e Li o indireto do preço marginal total pibi + Li.
Vale a nota que introduzindo o conceito de renda total, o problema de maximizar a utilidade sujeita às restrições de tempo e bens é resolvido em dois estágios: primeiro, a renda total é determinada a partir das restrições de bens e tempo e, em seguida, a utilidade é maximizada sujeita apenas à restrição imposta pela renda total.
Por trás da divisão em custos diretos e indiretos está a alocação de tempo e bens entre atividades voltadas para o trabalho e atividades voltadas para o consumo. Isso sugere uma divisão alternativa de custos; nomeadamente, nas resultantes da atribuição de bens e nas resultantes da atribuição de tempo. Escrevendo L_i = \partial L / \partial Z_i como

em que l_i = \partial L/\partial T_i e c_i = \partial L/\partial x_i são os ganhos marginais perdidos (sacrificados) de usar mais tempo e bens, respectivamente, em Zi.
A equação resultante da maximização pode então ser escrita como:

O custo marginal total de Zi é a soma de bi(pi + ci), o custo marginal do uso de bens na produção de Zi, e tili, o custo marginal do uso do tempo. Essa divisão seria equivalente àquela entre custos diretos e indiretos apenas se ci = 0 ou se não houvesse custos indiretos de uso dos bens.
A figura a seguir mostra o equilíbrio dado pelo resultado da maximização para um mundo de duas mercadorias. Em equilíbrio, a inclinação da curva de oportunidades de renda total, que é igual à razão dos preços marginais, seria igual à inclinação de uma curva de indiferença, que é igual à razão das utilidades marginais. O equilíbrio ocorre em p e p’ para as curvas de oportunidade S e S’, respectivamente.

Com isso, acabamos nossa exposição do modelo. Espero que tenham gostado e aprendido algo novo. Até a próxima.
Referência
Becker, Gary S. “A Theory of the Allocation of Time”. The Economic Journal 75.299 (1965): 493-517.
.
Leia também:
Inconsistência temporal – um exemplo
O modelo neoclássico de crescimento
Efeito da introdução de um imposto no equilíbrio de mercado
Evolução, racionalidade e transitividade




Deixe um comentário