A economia segundo a clássica definição de Robbins (1932) é a ciência que estuda o comportamento humano como uma relação entre fins e meios escassos com usos alternativos. A escolha nada mais é do que uma consequência da escassez, que segundo Alchian e Allen (2018) significa que nossos desejos superam os meios disponíveis para satisfazê-los, ou seja, escassez é produto dos nossos desejos ilimitados serem restritos seja pelas outras pessoas via competição, seja pela quantidade finita dos bens, seja pelo tempo.
Disso tudo deriva-se que é central para o cientista econômico entender como os agentes tomam suas decisões, como escolhem os fins e meios escassos, uma vez que, como dizem Castro e Faro (2005): “Um governo precisa antecipar as decisões dos contribuintes frente às regras tributárias que estiver determinando – e isso terá impactos não apenas em suas receitas mas também no desenvolvimento do país. Um gerente precisa antecipar as decisões de compra de seus clientes em função dos preços que escolher.” Ou seja, é preciso de um modelo para poder antecipar as decisões dos agentes, e é precisamente isso que abordaremos no presente artigo. Entraremos na teoria da escolha (ou teorias da decisão) para chegar na demanda de mercado por um bem.
Para essa tarefa será necessário o uso de matemática. Para tornar mais fácil ao leitor, iremos deixar todas as demonstrações dos teoremas no apêndice. Seguiremos de perto o livro “Models in Microeconomics Theory“, de Martin J. Osborne e Ariel Rubinstein.
Para facilitar as coisas, vamos supor que no mundo só existem dois bens, x e y. Vamos chamar de X o espaço que contém todas as combinações entre esses dois bens — a esse espaço damos o nome de “Espaço de Consumo”. Cada combinação entre quantidades desses dois bens chamaremos de “Cesta de Consumo”. Podemos, então, relacionar cada cesta de consumo do espaço X ao par ordenado (x,y). Se você não sabe o que é um par ordenado, vale a pena dar uma olhada nessa aula do Projeto Matemática.
Já que definimos o que são cestas de consumo, podemos agora criar uma relação entre elas. Essa relação deve ter algumas propriedades que reflitam a realidade da teoria que queremos expor, bem como permitir que construamos um modelo robusto. Chamaremos essa relação entre as cestas de “R”.
Para a relação binária R, a expressão xRy significa que x está relacionado a y de maneira R. Em economia queremos a relação entre as cestas dos bens, então adotamos como primitivo a preferência dos indivíduos. Desta derivamos uma escolha:
x ≽ y : denota que x é ao menos tão desejado quanto y, ou seja, a pessoa prefere x a y ou é indiferente entre x e y. Chamaremos essa relação de preferência fraca.
Dessa relação derivamos outras duas propriedades:
x ∼ y se ambos x ≽ y e y ≽ x. Esse símbolo denota que x é indiferente a y.
x ≻y se x ≽ y mas não y ≽ x. Esse símbolo denota preferência estrita de x a y.
Para podermos construir o nosso modelo, temos que supor algumas características da nossa relação (R):
Axioma 1: Relação binária completa.
Uma relação binária R no conjunto X está completa se para todos os membros x e y de X, tem-se que ou xRy ou yRx (ou ambos). Uma relação binária completa é, em particular, reflexiva: para cada x ∈ X temos xRx.
Axioma 2: Relação binária transitiva.
Uma relação binária R no conjunto X é transitiva se para quaisquer membros x, y e z de X para o qual xRy e yRz, temos xRz.
Axioma 3: Relação binária reflexiva.
Uma relação binária R no conjunto X é reflexiva se para quaisquer membros x de X, tem-se que xRx é tão bom quanto xRx.
Agora estamos prontos para definir um dos conceitos mais importantes no modelo que estamos construindo.
Definição 1: Relação de preferência.
Dado o espaço de consumo X, uma relação “R” entre cestas de consumo nesse espaço será uma relação de preferência se for completa, reflexiva e transitiva.
Quando modelamos decisões dos indivíduos, tomamos como dadas as relações de preferência. Mas para podermos operacionalizar em cima dessas preferências, é mais fácil usarmos números ao invés de algo como uma tabela que indique quais são as cestas preferidas às quais. Para isso, os economistas teóricos perceberam que é possível vincular um valor numérico a cada cesta, de modo que, quanto mais preferida a cesta é, maior será o seu valor. A essa função numérica damos o nome de função utilidade.
Definição 2: Função utilidade.
Para qualquer conjunto X e relação de preferência ≽ em X, a função u: X → R representa ≽ se:
x ≽ y se e somente se u(x) ≥ u(y ).
Dizemos que u é a função utilidade para ≽.
É digno de nota que a utilidade é ordinal e não cardinal, ou seja, os números que representam a satisfação do indivíduo ao consumir o bem são arbitrários. Sendo assim, o que importa é a ordem. Se x ≽ y, pouco importa se u(x) é igual a 2 ou 100 ou se u(y) é igual a -100 ou 0,05. O que importa para nós é que u(x) seja maior que u(y) dado que x é preferido a y.
Dadas as definições até agora, vamos estabelecer a seguinte proposição:
Proposição 1 (representação da relação de preferência por função de utilidade): Cada relação de preferência num conjunto finito pode ser representado por uma função utilidade.
Munidos da função de utilidade e de relações de preferência, podemos adentrar na teoria da escolha para construir nosso modelo de decisão individual e derivar disso a demanda do mercado. Lembrando que as relações de preferência dizem respeito apenas às atitudes mentais do nosso agente — por exemplo se ele prefere pizza ou hambúrguer, pepsi ou coca, prazer de fumar ou mais saúde no longo prazo, etc. Para saber do motivo pelo qual as escolhas são feitas temos que construir um aparato teórico próprio.
Formalmente, seja X o conjunto de todas as alternativas que um indivíduo pode enfrentar. Um problema de escolha é um subconjunto não vazio A de X, a partir do qual o indivíduo escolhe uma alternativa. Uma função de escolha descreve a escolha do indivíduo para cada problema de escolha possível.
Definição 5: Problema de escolha e função de escolha.
Dado um conjunto X, um problema de escolha para X é um subconjunto não vazio de X e uma função de escolha para X associa a cada problema de escolha A ⊆ X um único membro de A (o membro escolhido).
Em economia, nós conectamos o comportamento individual do indivíduo às suas atitudes mentais ao assumir que ele é racional, ou seja, que tal indivíduo tem uma relação de preferência em X. Isso significa que quando ele toma uma decisão ele está ciente das opções e assim escolhe a alternativa que é melhor, de acordo com a relação de preferência dele sobre o conjunto de possíveis alternativas.
Se a relação de preferência de um indivíduo é representada pela função de utilidade u, então o indivíduo age como se maximizasse a função u sob a restrição de que x, sua cesta escolhida, pertença a A. Formalmente, escrevemos seu problema como:
Max {u(x): x ∈ A}
Muito se critica a economia a respeito desse aspecto. Os críticos dizem que na verdade ninguém realmente age maximizando sua função de utilidade. Mas essa crítica falha em compreender que em nosso modelo o que importa é descrever o comportamento. Essa roupagem matemática da decisão no fundo só é um jeito de descrever como se os agentes agissem de uma dada maneira. Para uma resposta curta porém satisfatória a essas críticas, leia esse texto. Para uma defesa mais minuciosa das ditas hipótese irrealistas na economia, recomenda-se fortemente Friedman (1953).
Definição 6: Função de escolha racionalizável.
Uma função de escolha é racionalizável se houver uma relação de preferência tal que para cada problema de escolha a alternativa especificada pela função de escolha é a melhor alternativa de acordo com a relação de preferência.
Exemplo:
Seja X = {a, b, c}. A função de escolha que atribui “a” para {a, b, c}, “a” para {a, b}, “a” para {a, c} e “b” para {b, c} é racionalizada pela relação de preferência ≽ para a qual a ≻ b ≻ c. Ou seja, podemos descrever o comportamento de um indivíduo com esta função de escolha como se ele sempre escolhesse a melhor alternativa disponível de acordo com ≽.
Por outro lado, qualquer função de escolha que atribua “a” para {a, b}, “c” para {a, c} e “b” para {b, c} não é racionalizável. Se esta função de escolha pudesse ser racionalizada por uma relação de preferência ≽ então a ≻ b, b ≻ c e c ≻ a, o que contradiz a transitividade (axioma 2).
Além de tudo que foi feito até agora, é preciso introduzir uma nova propriedade ao nosso modelo, que é a propriedade α.
Definição 7: Propriedade α.
Dado um conjunto X, uma função de escolha c para X satisfaz a propriedade α se para quaisquer conjuntos A e B com B ⊂ A ⊆ X e c(A) ∈ B tivermos c(B) = c(A).
Ou seja, se um agente escolhe uma cesta de bens específica em um conjunto de cestas disponíveis, então num conjunto mais restrito onde ainda tiver a cesta escolhida originalmente, essa ainda será escolhida.
Dadas essa propriedades, podemos chegar a duas proposições:
Proposição 2 (função escolha racionalizável satisfaz propriedade α): Toda função escolha racionalizável satisfaz a propriedade α.
Proposição 3 (função escolha que satisfaz a propriedade α é racionalizável): Se X for um conjunto finito, então qualquer função de escolha para X que satisfaça a propriedade α é racionalizável.
A pressuposição de que toda a função escolha é racionalizável é geralmente defendida pelo fato de que comportamento não-racionalizável pode gerar prejuízos aos indivíduos. Um argumento clássico favorável a essa proposição é um argumento do tipo evolucionário feito por Alchian (1950). Nesse argumento se defende que o mercado doutrina os agentes para que suas escolhas sejam racionalizáveis, uma vez que num mercado competitivo os indivíduos que agissem de maneira racionalizável iriam ser selecionados pelo mercado. Sendo assim, no longo prazo só restariam no mercado escolhas racionalizáveis.
Segundo Osborne e Rubinstein (2020): ”Suponha que X consista em três alternativas, a, b e c, interpretadas como objetos, e que a função de escolha de um indivíduo atribua “a” para {a, b}, “b” para {b, c} e “c” para {a, c}. Uma implicação dessa função de escolha é que, para qualquer objeto x, se o indivíduo possui x, então existe um objeto y tal que o indivíduo deseja trocar x por y; dado que ele prefere y a x, ele está disposto a pagar uma quantia (possivelmente pequena) de dinheiro para fazer a troca. Suponha que, para cada troca, essa quantia seja de pelo menos $ 1. Nesse caso, um manipulador poderia primeiro dar “a” ao indivíduo, em seguida, oferecer a substituição de “a” por “c” em troca de $ 1, então oferecer a substituição de “c” por “b” em troca de outro $ 1 e, em seguida, oferecer a substituição de “b” por “a” por outro $ 1. Após essas três trocas, o indivíduo detém “a”, como fez inicialmente, e está $ 3 mais pobre. O manipulador pode repetir o exercício, tirando quanto dinheiro do indivíduo quiser. Esse mecanismo é conhecido como bomba de dinheiro (money pump).”
Esse argumento mostra que ter preferências inconsistentes prejudica o indivíduo e, no longo prazo, num mercado competitivo, faz com que ele saia do mercado, de modo que sobrem apenas agentes cuja regra de decisão é racionalizável.
Agora que construímos nosso aparato de preferências e escolhas, podemos adentrar na teoria econômica padrão, que é o indivíduo contemplando uma escolha entre bens.
Consideramos o conjunto X de todas as alternativas (entre dois bens) que um consumidor pode enfrentar como sendo o espaço R²+, o conjunto de todos os pares de números não negativos. Nos referimos a um elemento (x, y) ∈ X como uma cesta e o interpretamos como um par de quantidades de dois bens, chamados x e y.
Definição 8: Conjunto de alternativas (cesta)
O conjunto de alternativas é X = R²+. Um membro de X é uma cesta.
A cesta nada mais é que um par ordenado de bens, como pizza e hambúrguer, Pepsi e Coca ou bens intangíveis como prazer de fumar e mais saúde no longo prazo. As preferências em X refletem o trade-off entre os bens.
Dada a definição de cesta, podemos adentrar nas curvas de indiferença (ou conjunto de indiferença). A curva indiferença definida para o relação de preferência ≽ e a cesta “a” é o conjunto {y ∈ X: y ∼ a}, isto é, o conjunto de todos as cestas indiferentes de a. A coleção de todos os conjuntos indiferentes é a partição induzida pela relação de equivalência ∼. Se ≽ é representado por uma função de utilidade u, a indiferença definida para a cesta “a” pode alternativamente ser expressa como {y ∈ X: u(y) = u(a)}, que é o contorno de u para a cesta “a”. As curvas de indiferença podem ser ilustradas com a seguinte imagem:

Não discutiremos a fundo as propriedades das relações de preferências, mas elas são: (i) monotonicidade forte; (ii) continuidade; (iii) convexidade; e (iv) diferenciabilidade. Sugerimos ao leitor o capítulo 4 do Osborne e Rubinstein (2020) para uma elaboração minuciosa dessas propriedades.
Um problema de escolha para um consumidor é o conjunto de cestas que ele pode comprar, dados os preços e sua riqueza. Referimo-nos a este conjunto como o conjunto de orçamento do consumidor. Mais precisamente, dados os preços px e py e a riqueza I, o conjunto do orçamento do consumidor é o conjunto de todos as cestas que o consumidor pode obter trocando I pelos bens às taxas de câmbio fixas de px unidades de riqueza por uma unidade do bem x e py unidades de riqueza para uma unidade do bem y.
Definição 9: Conjunto orçamento (restrição orçamentária).
Para quaisquer números positivos px, py e I, o conjunto de orçamento (restrição orçamentária) de um consumidor com riqueza I quando os preços são (px, py) é
B((px,py),I) = {(x,y) ∈ X: pxx + pyy ≤ I}
Tal conjunto pode ser ilustrado com a seguinte imagem:

O conjunto {(x, y) ∈ X: pxx + pyy = I} é a linha de orçamento do consumidor. Esse conjunto está desenhado abaixo.
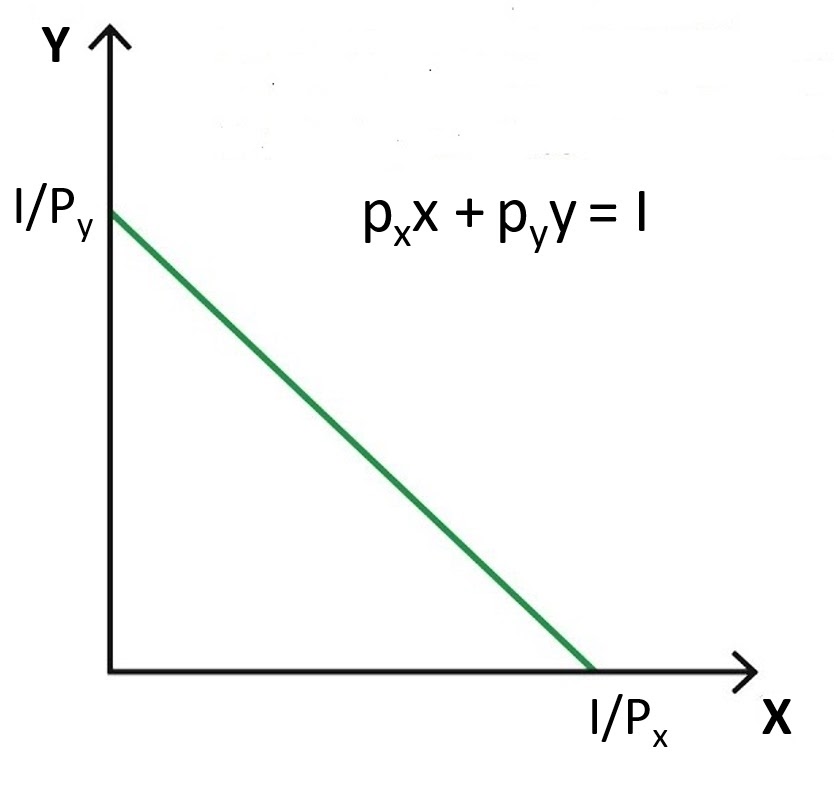
Vamos agora finalmente para a demanda, que nada mais é que uma regra de decisão racionalizável com as seguinte propriedades: a função de escolha do consumidor, chamada de função demanda, atribui a cada conjunto de orçamento um de seus membros. Um orçamento aqui é definido por um par ((px, py), I) com px, py e I positivos. Assim, o comportamento de um consumidor pode ser descrito como uma função de ((px, py), I).
Definição 10: Função demanda.
Uma função demanda é uma função x que atribui a cada conjunto de orçamento um de seus membros. Defina x((px, py), I) como o elemento atribuído ao conjunto de orçamento B((px, py), I).
Um consumidor racional nada mais é do que aquele que tem uma relação de preferência fixa (para uma defesa mais minuciosa dessa tese recomenda-se Becker e Stigler (1977)) e que para qualquer conjunto orçamentário ele escolhe a melhor cesta de acordo com sua preferência. Essa problemática de achar a melhor cesta no conjunto orçamentário recebe o nome de problema do consumidor.
Definição 11: Problema do consumidor.
Para uma relação de preferência ≽ em R²+ e números positivos px, py e I, o problema do consumidor é o problema de encontrar a melhor cesta de consumo no conjunto de orçamento B((px, py), I) de acordo com ≽. Se ≽ for representado pela função utilidade u, este problema é:
max (x,y)∈X u(x,y) sujeito a pxx + pyy ≤ I
O problema pode ser representado com a seguinte figura:

Nenhum ponto da curva da indiferença que passa dentro do conjunto orçamentário é a cesta escolhida, pois há ainda outras cestas que provêm mais utilidade ao indivíduo e que ainda pertecem ao conjunto orçamentário que não o ponto B, por exemplo. A cesta escolhida não é C, pois essa, embora entre as opções da imagem é a preferida, não pode ser selecionada dado o orçamento do indivíduo. O que nos resta como a opção de cesta ótima é aquela que tangencia a linha do orçamento, ou seja, o ponto A.
A demanda nada mais é a disposição a pagar do indivíduo. Ou seja, em termos do que colocamos até agora, a demanda é como a decisão ótima de consumo de um bem muda quando se tem alterações nos preços relativos. Derivando graficamente a curva de demanda temos:

Como mostra Becker (1962), o fato da curva de demanda ser negativamente inclinada não é uma consequência do pressuposto de racionalidade, pois independentemente da regra de decisão que o agente tomar, seja racional ou irracional, a demanda ainda assim será negativamente inclinada. Esse resultado é uma consequência da escassez, bastando que a cesta de consumo nova escolhida seja positivamente relacionada com a nova disponibilidade de bens, dada uma mudança nos preços relativos.
E a curva de demanda do mercado nada mais é que a soma horizontal das curvas de demanda dos participantes do mercado. Por exemplo, numa economia com dois indivíduos a curva de demanda do mercado ficaria desse jeito:

Assim concluímos nossa exposição. Partimos de uma decisão individual baseada nas crenças subjetivas dos indivíduos e chegamos no comportamento de mercado. Do subjetivo ao objetivo. Obviamente, para o modelo ficar completo precisamos derivar a curva de oferta (derivamos ela nesse texto aqui).
Apêndice
Demonstração da proposição 1:
Para iniciar nossa demonstração precisamos primeiro de um lema.
Lema 1: Existência de alternativas mínimas e máximas.
Seja X um conjunto finito não vazio e seja ≽ uma relação de preferência em X. Pelo menos um membro de X é mínimo em relação a ≽ em X e pelo menos um membro é máximo.
Prova:
Provamos o resultado para a minimalidade; o argumento para a maximalidade é análogo. Usamos a indução no número n de membros de X. Se n = 1, o único membro de X é mínimo em relação a ≽ em X. Suponha que o resultado seja verdadeiro para n-1. Provaremos que é verdadeiro para n. Seja y um membro arbitrário de X e seja x mínimo em relação a ≽ em X\{y} (um conjunto com n-1 membros). Se y ≽ x então x é mínimo em X. Caso contrário, então x ≽ y. Pegue qualquer z ∈ X\{y}. Como x é mínimo em X\{y}, temos z ≽ x. Portanto, por transitividade z ≽ y. Assim, y é mínimo em X, e a prova está concluída.
Provando a proposição: seja X um conjunto finito e seja ≽ uma relação de preferência em X. Seja Y0 = X e defina M1 como o conjunto de alternativas mínimas em relação a ≽ em Y0. Pelo Lema 1, Y0 não é vazio. Para k ≥ 1, indutivamente defina Yk = Yk − 1\Mk desde que Yk − 1 seja não vazio, e seja Mk + 1 o conjunto (não vazio) de alternativas mínimas em relação a ≽ em Yk. Em outras palavras, em cada estágio remova do conjunto de alternativas restantes as alternativas mínimas em relação a ≽.

Desde que Yk não seja vazio, pelo Lema 1 o conjunto Mk + 1 não é vazio. Como X é finito, para algum valor de K o conjunto YK é vazio (mas o conjunto YK −1 não é vazio). Assim, todo x ∈ X é membro de algum conjunto Mk para algum k, 1 ≤ k ≤ K.
Defina a função u: X → R por u (x) = k para todo x ∈ Mk, k = 1,. . . , K. Ou seja, anexe a cada alternativa o número do estágio em que ela é removida de X. Argumentamos que u é uma função de utilidade para ≽. Ou seja, para quaisquer alternativas “a” e “b” temos a ≽ b se e somente se u(a) ≥ u(b).
Temos u(a) = u(b) se e somente se a e b forem mínimos em relação a ≽ em Yu(a) −1, de modo que b ≽ a e a ≽ b e, portanto, a ∼ b.
Temos u(b) > u(a) se e somente se “a” for mínimo em relação a ≽ em Yu(a) −1, de modo que b ≽ a, e b ∈ Yu(a) −1, mas não é mínimo com em relação a ≽ em Yu(a) −1, de modo que não é o caso de a ≽ b. Portanto, b ≻ a.
C.Q.D.
Demonstração da proposição 2:
Seja c uma função de escolha racionalizável para X e seja ≽ uma relação de preferência tal que para cada conjunto A ⊆ X, c(A) é a melhor alternativa de acordo com ≽ em A. Suponha que B ⊂ A e c(A) ∈ B. Como c(A) ≽ y para todo y ∈ A, temos c (A) ≽ y para todo y ∈ B e, portanto, c(B) = c(A).
C.Q.D
Demonstração da proposição 3:
Seja c uma função de escolha para X que satisfaz a propriedade α. Denote por n o número de elementos em X. Construímos uma relação de preferência que racionaliza c como segue. Denote c(X) = a1, c(X\{a1}) = a2, c(X\{a1, a2}) = a3 e assim por diante. Ou seja, ak é a escolha do conjunto X após a remoção dos elementos a1,. . . , ak − 1.
Considere a relação de preferência ≽ definida por a1 ≻ a2 ≻ ··· ≻ an. Seja A um problema de escolha. A melhor alternativa em A de acordo com ≽ é o primeiro membro de A na sequência a1, a2,. . . , an, que seja am. Por construção, c({am, am + 1,…, An}) = am e como A ⊆ {am, am +1,. . . , an} e am ∈ A, da propriedade α temos c(A) = am.
C.Q.D.
Referência
Robbins, Lionel. “The nature and significance of economic science.” The philosophy of economics: An anthology. (1932): 73-99.
Alchian, Armen A., William R. Allen, and Jerry L. Jordan. Universal economics. Liberty Fund, 2018.
De Castro, Luciano I., e José Heleno Faro. Introdução à teoria da escolha. Vol. 250. IMPA, 2005.
Osborne, Martin J., Ariel Rubinstein. Models in Microeconomic Theory. Open Book Publishers, 2020.
Friedman, Milton. “The methodology of positive economics.” (1953).
Alchian, Armen A. “Uncertainty, evolution, and economic theory.” Journal of Political Economy. 58.3 (1950): 211-221.
Stigler, George J., and Gary S. Becker. “De gustibus non est disputandum.” American Economic Review. 67.2 (1977): 76-90.
Becker, Gary S. “Irrational behavior and economic theory.” Journal of Political Economy. 70.1 (1962): 1-13.
Leia também:
O problema da firma e a curva de oferta
O problema da informação assimétrica – O que é seleção adversa e risco moral
A economia dos fumantes
Modelo de oferta e demanda – o equilíbrio parcial e geral










Deixe um comentário