Lei da Demanda, Equação de Slutsky e Efeito Preço Puro de Becker

Dos meios através dos quais se manifestam aqueles que acreditam entender de economia, ouve-se falar em regras de “oferta e demanda”, ou ainda sobre as famosas “leis” que as governam. Talvez não saibam, mas este assunto decididamente não se encerra na retração do consumo da qual resulta o aumento do nível de preços.

Primeiramente precisamos ter o cuidado de não raciocinar a partir de uma mudança de preços, isto é, afirmar algo com base nas consequências da oscilação da nossa variável de interesse sem olhar para a causa desta variação.

Uma mudança de preços pode tanto aumentar o consumo quanto diminuí-lo! Vamos, por um momento, assumir que as curvas de oferta e demanda são “bem comportadas” (ou seja, as preferências são racionais, fortemente monótonas, estritamente convexas, homotéticas e contínuas – para saber mais, leia o apêndice matemático).

Embora, nesta situação, não seja necessário invocar preferências estranhas ou elasticidades, o caso não refuta a lei da demanda. Não devemos olhar a mudança do preço em si, mas a causa desta mudança! Por exemplo: um aumento dos preços produzido pela expansão da demanda acarreta no aumento da quantidade demandada. Em outras palavras, dada uma demanda fixa, com um aumento do preço, cai a quantidade demandada, ceteris paribus.

Lei da Demanda: Tudo ou mais constante, um aumento do preço do bem x implica uma diminuição na quantidade demandada do bem x.

Certo, mas o que está por trás dessa Lei da Demanda? Essencialmente, uma mudança de consumo decorrente de uma mudança de preços, correto? Mas ainda há dois efeitos importantes que merecem a nossa atenção. Refiro-me ao efeito substituição (ES) e ao efeito renda (ER). Ambos podem ser derivados pela equação de Slutsky.

O efeito substituição é a taxa que mede a variação do consumo quando ocorre uma mudança de preço; já o efeito renda mede a variação do poder de compra do consumidor quando há uma mudança de preços. Para ambos os efeitos, se considera a cláusula ceteris paribus. A equação de Slutsky calcula, então, o efeito-preço (EP). [De onde vem a curva de demanda? Para uma exposição mais minuciosa, leia aqui.]

A demanda é uma função que é derivada do problema do consumidor. Mas o que é esse problema? Veremos.

Problema do consumidor

O problema do consumidor é encontrar a cesta de bens que maximize sua função de utilidade sujeita à restrição, sendo a função utilidade apenas uma representação numérica das relações de preferência dos indivíduos. Tal problema pode ser representado genericamente da seguinte maneira:

Ao resolver o sistema, chegamos às demandas marshallianas:

Recebem este nome em homenagem ao economista mais famoso a derivá-las graficamente, que formulou a Lei da Demanda como entendemos hoje, que foi Alfred Marshall (1890,1892). Para saber como derivá-la, veja o apêndice.

As demandas ótimas [o apóstrofe (*) denota otimização] correspondem a uma função do preço e da renda. Daí deriva a intuição por trás da “equação de Slutsky”. Por um instante, suponha que tenha havido um aumento na quantidade do bem 1. Por consequência, tem-se uma mudança na quantidade demandada.

Mas com a mudança no preço também ocorre uma mudança na renda da qual resulta uma mudança na quantidade demandada. Por isso, uma simples mudança no preço gera, paralelamente, dois efeitos: o efeito renda (mudança no consumo em função da variação da renda) e o efeito substituição (mudança no consumo em função da variação do preço), sendo a mudança observada um efeito composto desses dois.

Para se chegar à equação de Slustky, é preciso entender sobre a demanda compensada ou demanda hicksiana, que seria justamente a demanda marshalliana quando eliminamos o efeito renda, focando apenas no efeito substituição. Como chegar até ela?

Vale lembrar que para chegar na curva de demanda, resolvemos o problema do consumidor, cuja lógica é simples: temos uma restrição orçamentária que limita as nossas possibilidades de consumo. Dadas as nossas preferências, e, portanto, função utilidade, queremos escolher a cesta de bens que provêm a maior utilidade. Graficamente é o mesmo que escolher o nível da curva que tangencia a restrição.

Como dito em outro texto: a demanda nada mais é do que a disposição dos indivíduos a consumir. Ou seja, a demanda verifica, na prática, a mudança da decisão ótima segundo o consumo quando se alteram os preços relativos. Derivando graficamente a curva de demanda temos:

Mas, para todo problema de maximização, podemos, também, pensá-lo como um problema de minimização, pelo qual a função-objetivo do primal (problema de maximização) é a restrição do dual (problema de minimização) e a restrição do primal é a função-objetivo do dual. Ou seja, ficamos com o seguinte, tomando novamente as mesmas utilidades do primal:

Analogamente, podemos representar esse problema da seguinte maneira:

Ou seja, o dual do problema do consumidor é justamente fixar um nível de utilidade a partir do qual seja possível minimizar a reta orçamentária até tangencia-la à de utilidade; minimizar o dispêndio para achar as quantidades ótimas. [Para saber como chegar a esse resultado, veja o apêndice matemático.]

Sendo assim, no dual, as quantidades ótimas encontradas são as demandas hicksianas, que recebem este nome em homenagem ao trabalho do economista John Hicks (1939).

Perceba que essa demanda não é mais uma função da renda. A intuição é a de que estamos compensando a perda de renda para que o indivíduo escolha a quantidade demandada do bem preservando o seu nível de utilidade original. Sendo assim, qualquer efeito da mudança de consumo do bem é fruto única e exclusivamente da variação dos preços e não da renda. Eliminamos o efeito renda e mantivemos apenas o efeito substituição, ou seja, a variação na quantidade consumida do bem x é quanto ele substitui sua taxa de x pela taxa de y.

Graficamente a derivação da curva de demanda hicksiana é a seguinte:

Tendo as demandas marshallianas e compensadas, para chegar à equação de Slutsky é preciso saber de mais alguns termos e equações. Comecemos com a função dispêndio, que seria a seguinte:

Substituindo as variáveis independentes pelas suas quantidades ótimas, temos:

Essa é a função dispêndio minimizada.

No ótimo, a quantidade demandada segundo a demanda marshalliana é a mesma que segundo a demanda hicksiana. Por isso, o primal e o dual chegam (e têm de chegar) ao mesmo resultado. Então, no ótimo, temos que:

Assim como as quantidades demandadas têm de ser iguais, ou seja,

Temos que:

Agora sim podemos chegar à equação que queríamos.

A Equação de Slutsky

Faremos a derivação completa aqui (e não no apêndice). Portanto, peço aos leitores um pouco de calma. Sabemos que no ótimo temos as seguintes equações:

Assim como sabemos que:

Então, a partir disso, uma variação no preço implica:

Por (1) e (2), podemos reescrever a equação acima por:

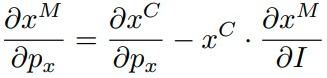
Sua versão no equilíbrio nada mais é que:

Chegamos na Equação de Slutsky! Ela nos ajuda a decompor o efeito-preço, isto é, como as mudanças de preço afetam a quantidade demandada em dois efeitos (renda e substituição). A partir destes, podemos avaliar o comportamento de consumo do agente frente a esse bem, sendo que, a depender de qual dos dois efeitos for o “dominante”, sabemos dizer se o bem é normal, inferior ou de Giffen.

Bem normal

Um bem dito normal é um bem cujo consumo aumenta quando a renda do indivíduo também aumenta. Por isso é normal, uma vez que a maioria dos bens que consumimos são deste tipo. Para garantir essa propriedade é preciso que tanto o efeito renda quanto o efeito substituição seja menores do que zero.

Graficamente temos o seguinte cenário:

A lógica da imagem é a seguinte: o indivíduo estava consumindo a cesta A sob a reta da  restrição orçamentária vermelha. Com a mudança do preço do bem x, ele se desloca para a curva azul, onde, sob essa nova restrição, o consumidor escolhe a cesta B.

O efeito preço (composto) é justamente esse deslocamento do consumo de A para B. Para ver quanto o indivíduo substituiu o consumo do bem x pelo consumo do bem y, portanto, deve-se calcular o efeito substituição. Deve-se, dados os novos preços relativos, deslocar a nova reta de restrição orçamentária para a curva de indiferença original. Assim, avaliamos que sobre a mesma utilidade o quanto o indivíduo consumiria de x com os novos preços. Enquanto isso, o resto da variação no consumo do bem x de C para B é dado pela diminuição na renda, portanto consequência do efeito renda.

Bem inferior

Um bem dito inferior é um bem cujo consumo diminui quando a renda do indivíduo aumenta. Por isso é inferior: pois quando a renda do agente sobe, este passa a consumir bens normais. Um exemplo comum deste tipo de bem é o transporte público. Para assegurar essa propriedade, é preciso que o efeito renda seja maior que zero, ao passo que o efeito substituição seja menor que zero.

Graficamente temos o seguinte cenário:

A diferença entre bem normal e bem inferior pode ser conferida na seguinte imagem:

Perceba que a direção da variação do consumo do bem em função do aumento da renda para o bem normal é a oposta à do bem inferior. Enquanto a variação do primeiro é positiva (Δx > 0) e do segundo se torna negativa (Δx < 0).

Bem de Giffen

Um bem de Giffen é uma anomalia, uma possibilidade meramente teórica que, até onde se sabe, não existe na realidade. Este bem seria um bem cujo aumento do preço levaria a um aumento da quantidade demandada. Há quem diga que isto seria uma refutação à Lei Geral da Demanda. Em relação a isso, tenho sérias dúvidas. De qualquer forma, para se obter este resultado, é preciso que o bem seja inferior e que o módulo do efeito renda seja maior que o módulo do efeito substituição.

Graficamente temos o seguinte cenário:

Para entender mais sobre os bens de Giffen, recomendamos o seguinte texto do professor Peñaloza.

Efeito Preço-Puro de Becker

Uma questão importante introduzida na literatura por Gary Becker (1962) é o efeito preço-puro. Segundo Becker, na decomposição feita por Slutsky, computa-se o efeito composto na quantidade demandada via preços, mantendo os outros constantes, e via renda. Todavia, para o efeito relevante é preciso considerar a renda real. Qual é a lógica?

Imagine as seguintes cestas:

Dada a mudança de preços, queremos achar a (nova) linha de restrição orçamentária que passa pela cesta original, uma vez que tem que ser factível e com a nova inclinação:

Logo, temos que

Assim,

Manipulando os termos, chegamos à seguinte expressão:

Mas quanto é \beta?

Ou seja, \beta nada mais é que o índice de preços de Laspeyres. Portanto, feita a correção, chegamos à seguinte solução gráfica:

Sendo assim, concluímos que:

Assim, com essa correção, garantimos que o efeito preço esteja sob condição ceteris paribus. Para entender melhor esse efeito, recomendo este vídeo do professor Peñaloza.

Com isso, terminamos nossa exposição da Lei da Demanda, equação de Slutsky e do efeito-preço puro de Becker. Até a próxima!

Apêndice matemático

Curvas de demanda bem comportadas

Seja o espaço de consumo X, que representa o conjunto de todas as possíveis (mutuamente excludentes) alternativas que um indivíduo enfrenta ao tomar uma decisão. Então:

x ≽ y denota que x é ao menos tão desejado quanto y, ou seja, a pessoa prefere x a y ou é indiferente entre x e y. Chamaremos essa relação de preferência fraca.

Dessa relação derivamos outras duas propriedades:

x ∼ y se ambos x ≽ y e y ≽  x. Esse símbolo denota que x é indiferente a y.

x ≻ y se x ≽ y  mas não y ≽ x. Esse símbolo denota preferência estrita de x a y.

Definição: Uma relação de preferência ≽ em X é racional se as preferências foram completas e transitivas.

1. Preferências são completas se para todo x, y ∈ X, x ≽ y ou y ≽ x (ou ambos).
2. Preferências são transitivas se para todo x, y e z ∈ X, se x ≽ y e y ≽ z então x ≽ z.

Para entender melhor a intuição econômica por trás da transitividade, recomendo esse vídeo.

Definição: Uma relação de preferência ≽ em X é monótona se x ∈ X e y >> x implica que y ≻ x. É fortemente monótona se y ≥ x e y =/= x implica que y ≻ x.

Definição: Uma relação de preferência ≽ em X é localmente não saciável se para todo x ∈ X e todo \epsilon > 0, há um y ∈ X tal que ||y –  x|| ≤ \epsilon.

É possível demonstrar que se uma relação de preferência é fortemente monótona então ela é localmente não saciável.

Dada uma relação de preferência e a cesta de consumo x, o conjunto contorno superior de uma cesta x é o conjunto de cestas que são ao menos tão boas quanto x: {y ∈ X: y ≽ x}. O conjunto contorno inferior de x é o conjunto de todas as cestas que x é ao menos tão bom quanto y: {y ∈ X: x ≽ y}. Enquanto, o conjunto de indiferença contendo o ponto x é o conjunto de todas as cestas que são indiferentes a x, ou seja, {y ∈ X: y ~ x}.

Definição: Uma relação de preferência ≽ em X é convexa se para todo x ∈ X. o conjunto do contorno superior {y ∈ X: y ≽ x} é convexo; isto é, se y ≽ x e z ≽ x, então a*y + (1-a)*z ≽ x  para qualquer a ∈ (0,1).

Definição: Uma relação de preferência ≽ em X é estritamente convexa se para todo x ∈ X, nós temos que y ≽ x e z ≽ x e y =/= z implica a*y + (1-a)*z ≽ x  para qualquer a ∈ (0,1).

Definição: Uma relação de preferência ≽ em X é homotética se todos os conjuntos de indiferença estão relacionados por expansão proporcional ao longo dos raios, isto é, se x ~ y então a*x ~ a*y para qualquer a ≥ 0.

Definição: Uma relação de preferência ≽ em X é contínua se é preservada entre seus limites. Isto é para qualquer sequência de pares

temos que x ≽ y.

A partir de relações preferências (≽ em X) racionais, fortemente monótonas, estritamente convexas, homotéticas e contínuas pode-se demonstrar que disso se seguem curvas de demanda bem comportadas. Derivar este resultado vai além dos propósitos do presente texto, mas para saber mais dessa recomenda-se Mas-Colell et al. (1995) e Kreps (2018).

Derivando a demanda marshalliana

Vamos resolver o problema do consumidor com uma utilidade com a forma funcional de uma Cobb-Douglas. Ou seja,

A restrição orçamentária é:

Portanto, dadas essas variáveis, o problema do consumidor montado fica assim:

Ademais, sem perda de generalidade, supomos que:

Montando o Lagrangeano temos:

Sendo assim, chegamos nas seguintes Condições de Primeira Ordem (C.P.O.s):

Isolando \lambda em (1) e (2) temos, respectivamente:

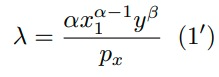
Igualando (1’) com (2’):

Ou seja, podemos derivar a seguinte expressão:

Substituindo (*’) em (3), temos:

O que acarreta nas seguintes demandas (marshallianas):

Derivando a demanda hicksiana

Tomando uma Cobb-Douglas de 2 bens e montando o Lagrangeano temos:

Sendo assim, chegamos nas seguintes Condições de Primeira Ordem (C.P.Os):

Igualando os \lambda temos que:

Por conveniência, chamemos a seguinte expressão de \gamma:

Portanto, da penúltima expressão podemos isolar os bens, de tal modo que chegamos nessas expressões:

Substituindo (2) em (1), temos

Portanto, por meio de algumas manipulações algébricas triviais, temos que:

Analogamente, substituindo (3) em (1) e isolando y temos

Referências

Marshall, Alfred. The Principles of Economics. McMaster University Archive for the History of Economic Thought, 1890.

Marshall, Alfred. Elements of economics of industry: being the first volume of Elements of Economics. Vol. 1. Macmillan and Company, 1892.

Slutsky, Eugenio. “Sulla teoria del bilancio del consumatore.” Giornale degli economisti e rivista di statistica (1915): 1-26.

Hicks, John R. Value and Capital: An Inquiry into Some Fundamental Principles of Economic Theory. Oxford: Clarendon Press, 1939, 2nd ed. 1946.

Becker, Gary S. “Irrational behavior and economic theory.” Journal of political economy 70.1 (1962): 1-13.

Dwyer, Gerald P., and Cotton M. Lindsay. “Robert Giffen and the Irish potato.” The American Economic Review 74.1 (1984): 188-192.

Mas-Colell, Andreu, Michael Dennis Whinston, and Jerry R. Green. Microeconomic theory. Vol. 1. New York: Oxford university press, 1995.

Kreps, David. Notes on the Theory of Choice. Routledge, 2018.

.

Leia também:
Teoria da escolha e curva de demanda
Teoria dos jogos – Alguns exemplos e aplicações
O problema da firma e a curva de oferta
Entenda o que são externalidades