O presente texto pretende nesta ocasião introduzir a teoria locacional da ciência econômica, que através de modelos microfundamentados procura demonstrar como é dada a escolha por parte das firmas referente ao local de instalação de uma nova unidade produtiva. O modelo apresentado será o triângulo locacional de Weber.
O modelo
O modelo possui as seguintes suposições:
Os mercados considerados estão em situação de concorrência perfeita;
As firmas levam em consideração a distância do centro consumidor e dos possíveis fornecedores ou centros de extração de matérias-primas;
A produção de uma firma n é dada por 2 insumos e vendida em 1 centro consumidor;
O custo de transporte é tido como constante e uniforme por todo o território.
Dadas as premissas, o modelo se baseia na figura geométrica de um triângulo, em que duas das pontas representam centros de fornecimento ou de extração de matérias-primas e a ponta restante representa o centro consumidor da firma considerada.
Seguindo assim, o ponto de ótima localização é dado por:
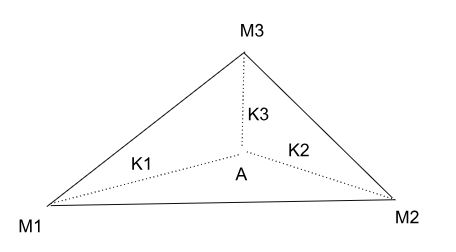
Em que:
M1 e M2 representam os centros de fornecimento;
M3 representa o centro de consumo;
A representa o ponto ótimo e é localizado na coordenada que minimiza os custos de transporte de M1, M2 e M3;
K1, K2 e K3 representam o custo por distância de transporte do ponto ótimo A até os pontos M1, M2 e M3.
Vamos considerar pesos distintos para cada variável. Recapitulando trigonometria, a função seno é uma função cíclica, variando de 0 a 1 até 90º e de 0 a 1 de 91º até 180º. Dessa forma, ao atribuir ao domínio de M1, M2 e M3 ângulos inferiores a 90º, o modelo consegue ponderar a distância de um ponto a outro multiplicando a distância equivalente pelo próprio seno do ângulo calculado.
Ademais, será suposto que a firma utilize na produção de seus bens proporções distintas de M1 e M2, sendo os pesos equivalentes n1 e n2. Será considerado também que a soma de n1 e n2 seja igual a 1.
Outra suposição é a de que todos os bens sejam transportados para o ponto M3, igualando assim o peso n3 a 1.
Pelo fato de que o somatório dos ângulos internos de um triângulo é 180, pode-se calcular os pesos da seguinte forma:
a1 = 180*\left(\dfrac{n1}{n1+n2+n3}\right)
a2 = 180*\left(\dfrac{n2}{n1+n2+n3}\right)
a3 = 180*\left(\dfrac{n3}{n1+n2+n3}\right)
em que a1, a2 e a3 são, respectivamente, os pesos de m1, m2 e m3.
Na sequência, desenha-se um triângulo abaixo do triângulo original considerando ângulos calculados:
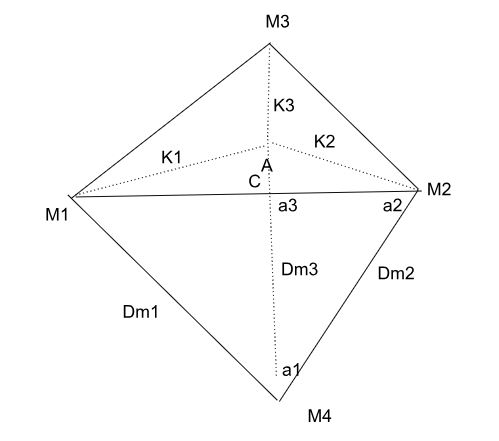
em que:
C é o ponto (0,0) do gráfico;
M4 é o ponto marcado para a existência do triângulo que possui os ângulos a1, a2, a3;
Dm1 e Dm2 são as distâncias dos pontos M1 e M2 até M4;
Dm3 é a distância de C até M4.
Dessa forma, o ponto A é localizado na seguinte coordenada:
O eixo x do ponto é obtido por: sen(a2)*Dm2 - Sen(a1)*Dm1;
Se negativo, o ponto se localiza à esquerda de M4; se positivo, à direita;
O eixo y é obtido por: sen(a3)*Dm3*d, em que d é o custo do transporte por unidade de distância.
Considerando o preço da terra
O modelo considera os preços da terra através do uso de isodapanas críticas, representadas ao redor do triângulo de maximização, de forma que quanto mais distante dos centros comerciais, maior o custo de transporte médio do produto no espaço.
A questão é que, quando uma firma qualquer se instala em uma localidade, o preço da terra sobe, fazendo com que os custos de instalação e de aluguel da terra também subam de forma que o novo ponto que minimiza os custos se dará numa localidade com maior custo de transporte.
O desenho geométrico das isodapanas ficará da seguinte forma:
em que a instalação da firma a encarece a terra na isodapana A, repelindo assim a firma b para a isodapana B.
Conclusão
O modelo locacional de Weber é um modelo matematicamente sólido e preciso, sendo um dos primeiros a conseguir abordar de forma razoavelmente significativa o processo de localização industrial. Porém, é necessário ressaltar suas premissas, de forma que o modelo se torna limitado quando considerado mercados concorrenciais imperfeitos e diferenciação dos custos de transporte.
No mais, o presente texto buscou esboçar introdutoriamente um modelo de economia espacial. Se o leitor tiver interesse em se aprofundar em modelos desse tipo, pode consultar as referências, colocadas abaixo.
Referências
ABLAS, Luiz Augusto. A Teoria do Lugar Central: Bases teóricas e evidências empíricas. São Paulo: IPE/USP, 1982.
MCCANN, P. Modern Urban and Regional Economics. Oxford: Oxford University Press, 2013.
Deixe um comentário