Introdução e contextualização teórica
Nosso objetivo neste texto consiste em apresentar o moderno modelo macroeconômico que pode ser particularmente útil para interpretar a usual política macroeconômica, especialmente o comportamento do Banco Central (BC), em um contexto institucional pautado por metas de inflação. Na literatura, o modelo foi “batizado” com as mais diversas denominações [neo-keynesiano, neo-keynesiano com preços rígidos, keynesiano sem a LM (Romer (2000)), etc.]. A denominação ou “carimbo” é bem menos relevante que a utilidade dele para compreender e avaliar a gestão que a maioria dos países faz de sua política macro ou política econômica de curto prazo.
Um ponto crucial do modelo (e possivelmente sua maior singularidade) consiste em colocar um novo paradigma na administração da Política Monetária (PM). No tradicional modelo IS-LM, a PM era gerenciada mediante o controle dos agregados monetários. Conforme fosse assumida a oferta agregada (OA), a alteração da oferta de moeda ou era responsável apenas pelo nível de preços ou podia alterar o nível de atividade ao custo de maior inflação. Nesse arcabouço, permeava a OA o funcionamento do mercado de trabalho. No caso de a oferta de trabalho estar pautada pelos salários reais (e não nominais, ou seja, sem ilusão monetária) e previsão perfeita, a OA era dada, o PIB se deduzia a partir do equilíbrio no mercado de trabalho. Neste mercado, determinavam-se salários reais e nível de emprego, nível de emprego que, via Função de Produção, determinava o PIB. Essa oferta encontrava sua demanda (Lei de Say) via taxa de juros. Ou seja, a taxa de juros era uma variável gerada no setor real da economia para nutrir uma demanda que esvaziasse a oferta. Nesse contexto, a oferta de moeda só determinava o nível de preços ou as magnitudes nominais do equilíbrio real previamente determinado. No topo da hierarquia situava-se o mercado de trabalho e, a partir desse equilíbrio, deduzia-se todo o setor real de economia. A moeda vinculava-se, apenas, à unidade de conta.
Nesse paradigma não existiria nenhum trade-off (nenhuma escolha). No caso de existir desemprego, este seria oriundo de alguma rigidez nos salários reais determinados no mercado de trabalho. Na medida em que a incompatibilidade entre oferta e demanda de trabalho (desemprego) se originava na dimensão do preço do trabalho (salários reais além do equilíbrio e que seriam inflexíveis à baixa), tanto a política fiscal quanto a PM não alterariam o nível de atividade.
Contudo, depois do artigo de Phillips (1958), uma relação negativa entre desemprego e inflação de salários nominais (preços) adquiriu consenso no mainstream [ex., Samuelson e Solow (1960)] e parecia ter certa aderência nos dados. A Curva de Phillips (CP) como policy menu impunha um desafio teórico maior no modelo não keynesiano ou clássico, uma vez que significava a possibilidade da política econômica alterar as variáveis reais. Ou seja, todo o modelo clássico caiaria por terra. A resposta, também teórica, foi dada por Friedman (1968) e Phelps (1967) com a denominada CP ampliada pelas expectativas ou CP aceleracionista. Neste caso podiam ser vislumbrados impactos de política econômica sobre o nível de atividade/desemprego com um custo: aceleração da inflação. Essa possibilidade surgia da provável distância entre os salários reais imaginados pelos assalariados no momento da sua oferta de trabalho e os realmente pagos. Esse erro, que surge da formação de expectativas, olhando para o passado (ou expectativas adaptativas), só podia ser transitório. Se no curto prazo há trade-off (o custo de menor desemprego seria a aceleração da inflação) no longo prazo essa escolha inexistiria e o equilíbrio se situaria sobre a taxa de desemprego “natural” ou de pleno emprego.
Nesse sentido, no curto prazo, a OA não seria vertical, fixa. Sempre em um horizonte de tempo de curto prazo, a OA teria uma inclinação positiva: maior inflação acompanharia maior nível de atividade/maior nível de emprego. Desse modo, a CP poderia ser uma proxy da OA.
Se agora dirigirmos nossa atenção à PM, o modelo IS/LM tradicional supunha que o BC controlava a oferta nominal de moeda e, nesse sentido, fixava a posição da LM. A taxa de juros nominal e real era igual, uma vez que os preços eram fixos, porém, o mais relevante, era um nível de taxa de juros que se determinava endogenamente.
Mas, na realidade, a PM tanto pode consistir no controle dos agregados monetários como na fixação da taxa de juros. Em um artigo pioneiro, Poole (1970) explora a PM ótima diferenciando a origem dos choques. Em um choque oriundo do setor real o melhor instrumento de política seria a oferta de moeda e, contrariamente, em um choque cuja raiz fosse o mercado de moeda a ferramenta a ser privilegiada seria a taxa de juros. Em termos teóricos, como levantaram Clarida, Galí y Gertler (1999), o problema seria: em que medida os choques são observáveis ou não. Uma vez que mudanças na demanda de moeda não são imediatamente observáveis, suas alterações não antecipadas induziriam a bruscas alterações nas taxas de juros, com significativos custos em termos do nível de atividade.
À margem desse debate de cunho mais teórico, em um famosíssimo artigo, Taylor (1993) apresenta uma expressão que sintetizaria a forma como os BC’s administram sua política monetária. A variável relevante para os objetivos da autoridade monetária não seriam mais os agregados monetários, senão a taxa nominal de juros. Essa transição entre fixar uma meta para a variação dos agregados monetários ou, contrariamente, apelar a outras ferramentas para atingir seus objetivos de gerenciamento da conjuntura, parece ter sido mais uma questão prática que ancorada em debate teórico. Uma frase de Gerald Bouey, Presidente do Banco Central do Canadá, quando, em novembro de 1982, essa instituição abandonou as metas de agregados monetários sintetiza bem a transição: “We didn’t abandon monetary aggregates, they abandoned us“. Essa transição entre o controle dos agregados monetários e a taxa de juros foi questionada pelo monetarismo clássico e várias frases de Friedman vão nesse sentido. Por exemplo Friedman (1968) disse: “These considerations not only explains why monetary policy cannot peg interest rates; they also explain why interest rate are such a misleading indicator of whether monetary policy is “tight” or “easy”. For that, it is far better look at the rate of change of the quantity of money”.
O certo é que, à margem do debate teórico, a observação de Taylor sobre o comportamento dos BC’s na prática foi incorporado nos modelos macro ainda que, posteriormente, como veremos mais na frente neste texto, o mesmo tenha obtido uma fundamentação micro e não simplesmente uma fórmula ad-hoc, representando o que se assume como a prática das autoridades monetárias. Essa passagem de uma fórmula mecânica ou empirista ou ad-hoc e uma fundamentação microeconômica tem desdobramentos no funcionamento do modelo. Neste texto apresentaremos uma síntese do modelo a partir de uma fundamentação micro. Deixamos para desenvolver em um próximo texto o modelo com a Regra de Taylor na sua versão mais empiricista, útil em uma versão mais simples do modelo e sua exposição gráfica.
O modelo
Basicamente o modelo consta de três equações.
A oferta agregada
Como já afirmamos, a CP pode ser assumida como uma proxy de oferta agregada. Em termos formais, vamos especificar a CP mediante a seguinte expressão:

onde:
\pi_t = taxa de inflação do período t;
\pi^e_t = taxa esperada de inflação para o período t;
y_t - y^{pe}_t = hiato do produto (em termos %) no período t, sendo pe o pleno emprego ou produto potencial;
\beta_\pi = coeficiente que indica a sensibilidade da inflação ao hiato do produto;
\varepsilon_s = choques temporários de oferta (aumento do preço dos alimentos por quedas da safra, guerras que alteram o aprovisionamento de energia, etc.)
No lugar do hiato do produto poderíamos trabalhar com a distância entre a taxa corrente de desemprego e a taxa natural. A Lei de Okun faz o elo entre o hiato do produto e o hiato entre taxa corrente de desemprego e taxa natural. Consideramos que desenvolver o modelo com o hiato do produto vai fazer a álgebra mais simples, uma vez que se colocamos a Lei de Okun teríamos que adicionar uma outra equação sem agregar nada em termos analíticos. Dessa forma, quando falarmos, por exemplo, que o PIB corrente está aquém do potencial, ( y_t - y^{pe}_t < 0 ), estamos supondo uma taxa de desemprego além da taxa de desemprego natural.
A relação entre inflação no período t e PIB é crescente e, na ausência de choques de oferta e quando o PIB é igual ao PIB potencial ( y_t = y^{pe}_t ) a inflação corrente é igual à inflação esperada. Choques de oferta ou mudanças nas expectativas deslocam a CP.
A IS
A função IS relaciona o nível de produto com a taxa de juros real, relação obviamente negativa. Concretamente temos:
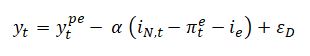
onde:
\alpha = sensibilidade do nível de atividade a variações na taxa real de juros;
i_{N,t} = taxa nominal de juros no período t;
i_e = taxa real de juros “natural” ou de equilíbrio;
\varepsilon_D = choques de demanda.
Vamos definir a taxa nominal de juros de equilíbrio ( i_{N,t} ) como sendo:

onde \pi_M é a meta de inflação.
Isso porque, teoricamente, em equilíbrio as expectativas têm que ser igual à meta ( \pi^e_t = \pi_M ), de onde se deduz a igualdade anterior. Lembremos desta expressão, uma vez que vamos a utilizar mais à frente.
Observemos que, quando a taxa real de juros ( i_{N,t} - \pi_t ) é igual à taxa natural, e na ausência de choques de demanda, o nível de atividade será igual ao nível de pleno emprego.
Há diferentes formas de especificar a IS. Por exemplo, no lugar de definir a taxa real de juros como sendo a nominal, descontada a inflação esperada, poderíamos colocar, como muitas vezes é apresentado, a taxa nominal menos a inflação corrente:

Contudo, é mais robusto analiticamente considerar que o consumo e/ou o investimento serão afetados não pela taxa real de juros considerando a inflação hoje, senão que pela inflação que os agentes imaginam no futuro. Por simplicidade, pode-se supor que \pi_t = \pi^e_t mas, sem dúvida, a taxa relevante é a esperada e não a corrente. Ou seja, vamos trabalhar com a expressão (2) e não com a (3).
Regra de Taylor (RT) e Regra Ótima de Política Monetária
Por último, poderíamos complementar o modelo com a RT, nome que advém do já mencionado artigo de Taylor (1993), onde o gerenciamento conjuntural dos BC’s está pautado tanto pelos desvios da inflação com respeito à meta quanto pelos desvios do PIB com respeito ao PIB potencial.
Em termos formais, a RT é:

O BC fixaria i_{N,t} (a taxa nominal de juros no período t) em função da taxa nominal, que no equilíbrio seria i_e + \pi_M , do hiato da inflação esperada com respeito à meta ( \pi_t^e - \pi_M ) e do desvio do produto em relação ao produto potencial, y^t - y_t^{pe} (ou, via Lei de Okun, em função dos desvios da taxa de desemprego com respeito ao nível natural).
Observemos que se o sistema está em equilíbrio ( \pi_t = \pi^e_t = \pi_M e y^t = y_t^{pe} ) a taxa real de juros ( i_{N,t} - \pi_t) será a taxa real de juros natural ou de equilíbrio ( i_e ).
O coeficiente \beta_{BC,\pi} representa a aversão do BC à taxa de inflação e o coeficiente \beta_{BC,y} a aversão ao desvio do produto (ou a uma elevada taxa de desemprego com respeito ao nível natural). No caso de o único compromisso do BC ser com a meta de inflação, tem-se \beta_{BC,y} = 0 . Este seria o caso de vários BC’s do mundo, que só teriam como mandato atingir a meta de inflação. Contudo, mesmo que em termos legais o compromisso do BC esteja reduzido à variação dos preços, na prática todos os BC’s não deixam de ter um olhar no desemprego. A relação \beta_{BC,\pi} / \beta_{BC,y} indicaria as ponderações respetivas.
Em algumas especificações da RT, no lugar de \pi^e_t - \pi_M é utilizado o desvio da inflação com respeito à meta ( \pi_t - \pi_M ). Mas essa expressão não é adequada, pois o BC tem que estar pautado por uma racionalidade forward-looking. Esse fato não esgota o debate, uma vez que a controvérsia se desloca ao indicador que o BC utiliza para determinar \pi^e_t . Escolher como parâmetro as projeções do setor privado ou do mercado financeiro já mereceu críticas até de teóricos do próprio mainstream [Bernanke e Woodford (1997)].
Essa forma de colocar a conduta do BC é ad hoc ou mecânica. Uma alternativa consiste em fundamentar microeconomicamente o comportamento do BC e encontrar o equilíbrio desse processo de administração da taxa nominal de juros.
Como é corriqueiro no arcabouço teórico do modelo canônico, é preciso definir uma função objetivo a ser maximizada ou minimizada e, simultaneamente, especificar uma restrição ou várias restrições. A Função Objetivo do BC seria minimizar os desvios do produto de seu potencial e a taxa de inflação de sua meta. Formalmente, teríamos:

Para simplificar a álgebra, normalizamos \beta_{BC,\pi} = 1 .
A restrição seria a CP, uma vez que essa relação representa o trade-off ao que o BC está submetido. Resolvendo o problema [(5) s.a. (3)], chegamos à seguinte expressão:

A expressão \frac{\beta_{BC,y}}{\beta_\pi} tem um significado econômico, uma vez que relaciona a aversão do BC ao hiato do produto com o “custo” ( 1/ \beta_{\pi} ) em termos de inflação, de alterar esse hiato, custo dado pela CP.
A expressão (6) seria a nossa Regra Ótima de Política Monetária.
Fechando o modelo
O modelo está constituído por três equações: (1), (2) e (6) com as variáveis endógenas y_t, i_{N,t}, \pi_t . A resolução do sistema é a seguinte:

Avaliação dos resultados
A primeira questão que chama a atenção é a característica da taxa de juros nominal ( i_{N,t}) determinada pelo BC. Esta é uma Regra de Política Monetária Ótima, deduz-se da minimização da Função Objetivo do BC sujeita à restrição da CP e integrada em um modelo macro. As três variáveis endógenas, y, i_{N,t}, \pi_t , determinam-se no modelo. Quando o BC fixa a taxa nominal de juros de curto prazo está fixando o nível de atividade e a taxa de inflação. Observemos que na expressão (7) não existe hiato do produto, como quando ad hoc colocamos a Regra de Taylor. Esse fato deriva da própria lógica deste arcabouço, uma vez que estamos lidando com um modelo macro onde o produto é endógeno. Ou seja, não pode existir hiato do produto exógeno. Exógeno é o produto potencial, mas se o produto é endógeno o hiato do produto tem que, necessariamente, ser endógeno também. A taxa de juros nominal de curto prazo vai estar em função do hiato entre as expectativas de inflação e a meta, mas não do hiato do produto.
O BC vai reagir a este último hiato de forma agressiva, uma vez que:

Este fato é conhecido como Princípio de Taylor e tem sua lógica. Caso haja uma deterioração das expectativas de inflação com respeito à meta, o BC teria que elevar a taxa real de juros e isso só é possível se o coeficiente que acompanha a expressão \pi_t^e - \pi_M seja maior que 1, como em (7).
Reparemos, por último, que a taxa nominal de juros de curto prazo se vê afetada positivamente tanto pelos choques de oferta como de demanda. Um erro usual consiste em supor que a taxa de juros nominal só vai ser afetada pelos choques de demanda e não os de oferta. Esse é um engano corriqueiro na discussão sobre a reação do BC a uma inflação que supera o limite superior da meta. Contudo, a reação do BC a um choque de demanda vai ser mais acentuada que a um choque de oferta da mesma magnitude.
.
Leia também:
A teoria econômica e o mercado de trabalho
Qual o juro de equilíbrio atual do Brasil?
Um toy model explicando como o Banco Central define a taxa básica de juros
Um modelo macroeconômico de livro-texto












Deixe um comentário