A Curva de Kuznets

“É preciso crescer o bolo para depois distribuí-lo.”
– Antônio Delfim Netto

Sumário

O que é a Curva de Kuznets?

A década de 60 foi um período turbulento para a história do Brasil. Nesse período, uma das frases que entrou para a história foi a célebre expressão acima proclamada pelo economista Antônio Delfim Netto. Por trás dela, há uma ideia que serviu para legitimar o modelo de crescimento econômico adotado pelo regime militar, que se desdobrou numa brutal desigualdade de renda. Mas qual é de fato a relação entre a desigualdade e crescimento? Desigualdade implica em crescimento? Crescimento implica em desigualdade? Ou há mais nuances nesta relação? Vamos tratar do que a teoria econômica e as evidências modernas têm a dizer sobre essa problemática.

Quando olhamos para a frase do Delfim Netto, encontramos na verdade apenas uma retórica para justificar as medidas promovidas pelos formuladores de políticas para legitimar a estratégia econômica de crescimento, a despeito dos possíveis efeitos na desigualdade. Mas há algo científico e verdadeiro nessa justificativa?

Implícita nela, há a teoria proposta pelo economista Simon Kuznets (1955) na década anterior, de que durante a trajetória do crescimento de um país, seu crescimento conduziria a uma maior desigualdade de renda até um certo ponto. A partir disso, os frutos da renda a mais iriam escoar para as diversas camadas da população acarretando numa menor desigualdade. Essa teoria em verdade é produto de uma inserção ad hoc na teoria econômica após a descoberta de Kuznets do fato estilizado que documenta a relação empírica entre desigualdade e crescimento. Tal relação empírica ficou conhecida como a Curva de Kuznets. Vamos investigar tal relação com base numa leitura próxima de Ray (1998).

A Curva de Kuznets é representada tendo no eixo horizontal o nível de renda dos países, y, e no eixo vertical, algum índice de desigualdade, I. Documenta-se uma relação de “u invertido” entre essas variáveis. Ou seja, a trajetória de crescimento dos países é tal que para níveis baixos de renda, os países têm baixa desigualdade; e na medida que eles começam a se desenvolver, a desigualdade aumenta. Há um ponto de crescimento intermediário no qual a desigualdade está no seu máximo, a partir do qual ela começa a cair conforme o país cresce. Então, em linhas gerais, quando o país tem baixa renda e baixa desigualdade, crescer e aumento da desigualdade se movem na mesma direção, até um ponto que partem em direções contrárias, convergindo para um país de alta renda e baixa desigualdade.

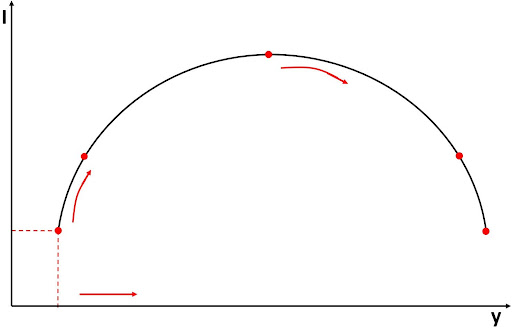
Explicação teórica para a existência da Curva de Kuznets

Qual é o significado da desigualdade ao longo da Curva de Kuznets? A curva está associada com uma ideia de um processo de desenvolvimento que é inclusivo, porém não é universal. Ou seja, na medida que a economia começa a se desenvolver, alguns setores da economia começam a se beneficiar primeiro desse desenvolvimento e daí outros setores vão sendo incorporados no processo. Essa transição advinda do crescimento com benefícios heterogêneos pela economia está associada a uma ideia dos anos 50/60 de crescimento dual, em que o crescimento da economia é marcado por uma transição de campo-cidade.

Tal transição se dá da seguinte maneira: nos baixos níveis de desenvolvimento dos países, o crescimento é predominantemente marcado por atividades agrícolas, ou seja do setor primário. Com o tempo, tem-se choques de tecnologia que vão tornando essa atividade agrária mais produtiva e a economia começa a ter mais recursos, que por sua vez, começam a fomentar o setor secundário, i.e., o setor de manufaturados, que é um setor de maior produtividade, que dá mais renda ao trabalhador e que integra uma parte da sociedade. As inovações tecnológicas na economia absorvem uma parte da população para esses setores novos. Na medida que a economia continua a se desenvolver com esses ganhos de produtividade, o setor de manufaturados, tipicamente associado a uma maior concentração urbana, maior divisão de trabalho, maior complexidade e diversidade de pautas de produtos produzidos, começa a atrair pessoas do campo para a cidade, dados os maiores níveis de remuneração. Enquanto o país segue se desenvolvendo, o setor vanguardista vai atraindo cada vez mais a população rural aos centros urbanos, assim como acaba levando maior produtividade ao campo pelas inovações tecnológicas, o que fomenta ainda mais esse processo migratório campo-cidade.

Há duas formas de se pensar em como a população do campo se beneficia dos ganhos de produtividade: primeiro, há uma migração do campo para a cidade, que leva aos migrantes se beneficiarem dos ganhos de produtividade; e depois o próprio campo acaba se beneficiando pela tecnologia da cidade, pois torna o trabalho no campo mais produtivo, elevando a remuneração desse setor.

Essa história de crescimento dual, em que a economia tem um setor arcaico e conservador e um setor moderno e pujante que puxa o crescimento da economia, leva a uma relação empírica entre desenvolvimento econômico e desigualdade confluente com a Curva de Kuznets. Isso se deve ao fato que no primeiro estágio a sociedade está totalmente empregada no setor agrícola, arcaico e de baixa produtividade. Na medida que o setor industrial começa a se desenvolver em segundo estágio, dada a produtividade maior, trabalhadores empregados no setor são melhor remunerados. Assim, há uma migração do campo para a cidade e, portanto, aumenta-se a desigualdade, dado o diferencial de remuneração entre os setores. Este processo continua até um ponto máximo de desigualdade, até que se chega em um estágio final no qual o setor conservador se beneficia dos ganhos de produtividade do setor avançado, seja por fatores migratórios, seja por questões envolvendo avanço tecnológico. Aumenta-se a remuneração do campo, que por sua vez acarreta numa diminuição da desigualdade.

Consequentemente, é por conta desses fatores que dizemos que essa trajetória de crescimento (dual) é inclusiva, uma vez que começa beneficiando um pequeno grupo de pessoas na sociedade e vai incorporando parcelas maiores. Além disso, não é universal, pois está contingente ao desenvolvimento do setor industrial, que puxa um crescimento cujos benefícios são heterogêneos.

Verificação empírica da Curva de Kuznets (Parte 1)

Como se documenta um padrão empírico desse tipo? Idealmente, gostaríamos de observar por janelas muito longas de tempo a desigualdade e a renda de vários países de forma a ter uma representação da curva para cada país na amostra. No entanto, há um problema de disponibilização de dados, pois não temos medidas de desigualdade dos países para períodos muito longos. Então temos que trabalhar com outras estratégias empíricas para fazer essa inferência, adotando algumas hipóteses, uma vez que não temos dados suficientes para fazer o que originalmente queríamos.

Primeiramente, vamos olhar o que temos de informação sobre essa relação. Uma primeira tentativa é olhar um corte transversal de países. Ou seja, pega-se uma amostra com vários países em um mesmo momento no tempo e se trabalha com a seguinte hipótese: um país com um nível alto de renda representa o contrafactual do país com baixa renda que ainda precisa percorrer sua trajetória de desenvolvimento. Então, se tirássemos uma foto do mundo, encontraríamos países desenvolvidos como Canadá, Austrália, Suécia, etc., que são países com alta renda e baixo nível de desigualdade. Do outro lado, teríamos países pobres como Cuba, algumas nações africanas e países asiáticos, que possuem baixo nível de renda e baixa desigualdade. Da mesma forma, encontraríamos uma gama de países de renda intermediária que possuem alta desigualdade, como países da América Latina.

Então, como se lê a estratégia do corte transversal? Se tirarmos uma foto dos países e pegarmos dados de renda e desigualdade, o que iremos encontrar é a relação de u invertido da Curva de Kuznets.

Lembrando que a Curva de Kuznets não é sobre o padrão da distribuição de países em um corte transversal, mas sim sobre a relação entre a trajetória de renda de um país e o seu nível de desigualdade. Sendo assim, toda vez que fazemos uma inferência sobre a trajetória de uma país e seu nível de desigualdade a partir de uma amostra de vários países, estamos usando a hipótese fundamental de que um país é contrafactual do outro, ou seja, a Suécia – país de alta renda e baixa desigualdade – é contrafactual de Cuba – país de baixa renda e baixa desigualdade -, se Cuba tivesse a renda da Suécia ou o contrário, i.e., Cuba é o contrafactual da Suécia se ela tivesse sua renda. Assim cada país seria contrafactual do outro em relação ao seu ponto na curva. Mas essa é uma boa hipótese? Ela é crível? Olhemos para as evidências.

A questão foi analisada e sintetizada em uma tabela de um estudo de Paukert (1973) que separa os países em intervalos de renda considerando o dólar americano em 1965 na primeira coluna. Na coluna seguinte tem-se o índice GINI médio dos países, e na terceira o intervalo do GINI, ou seja, o intervalo entre o menor e o maior GINI dos países no dado intervalo de renda considerado. O que percebe-se é que ao aumentar a renda, de fato a desigualdade medida pelo índice GINI aumenta até certo ponto, e depois começa a diminuir na medida que os países possuem maior renda. Então, pode-se afirmar que, na média, observa-se nos dados o padrão esperado da Curva de Kuznets.

Uma observação interessante da tabela acima é que o índice GINI mais alto dos países presente no menor intervalo de renda também repete um comportamento parecido com a curva de Kuznets, i.e., o maior índice aumenta conforme o aumento da renda, e em seguida começa a cair. Porém, o padrão do menor índice é mais instável, uma vez que não tem uma trajetória clara nos dados.

Esses são alguns fatos estilizados documentando sobre essa relação entre desigualdade e renda em um corte transversal de países. Mas quais são os cuidados que tem de ser tomados para interpretar esses fatos?

Cuidados com interpretações e documentação da Curva de Kuznets

1. Variabilidade nos dados

A primeira coisa a se observar quando se olha esse conjunto de países no corte transversal é que há uma grande variação entre a relação desigualdade e renda. Ou seja, os países não apresentam esse padrão de maneira bem definida, tendo uma variação substancial nos dados. Tal variação indica que podemos estar fazendo uma correlação espúria entre as variáveis elencadas. Por exemplo, se voltarmos para tabela, percebe-se uma grande dispersão nos dados, pois os intervalos do índice de GINI para cada uma das faixas de renda são bastante grandes, inclusive com sobreposição dos intervalos entre faixas de renda.

As variações e dispersões grandes indicam que apesar de encontrarmos um efeito médio que apresenta a relação esperada, mesmo assim não é uma relação muito precisa e, consequentemente, essa relação pode ser meramente espúria. Lembrando que estamos fazendo uma inferência sobre a trajetória de crescimento dos países e do seu nível de desigualdade com base em dados de países em um corte transversal, então há aqui uma hipótese muito forte de que um país é contrafactual do outro e não há razão crível para acreditar que é o caso (por exemplo, decorrente das diferenças institucionais e culturais entre os países).

Pode muito bem ser o caso de que, por exemplo, existam grupos de países que possuem uma relação estrutural positiva entre crescimento e desigualdade. Pode muito bem ser o caso que na verdade cada país tem sua própria trajetória de crescimento e desigualdade. Pode ser que a relação entre desigualdade e renda seja ausente na maioria dos países, e o que se observa nos dados é meramente uma coincidência do período registrado, sendo apenas uma correlação do momento que não diz nada estrutural sobre os países – mas é justamente essa evidência estrutural que queremos.

2. Especificações econométricas usadas para identificar a relação de Kuznets

Para identificar a Curva de Kuznets podem se usadas diferentes especificações econométricas, o que por sua vez pode gerar resultados diferentes, atrapalhando nossa inferência sobre o fenômeno em questão. Uma especificação traz uma forma quadrática em relação à renda:

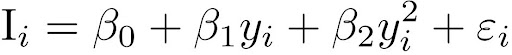
onde $I_i$ é a desigualdade do país i e $y_i$ é a sua renda; $\varepsilon_i$ é o termo de erro.

Nesta especificação esperaríamos que os resultados fitados sejam coerentes com a curva de Kuznets, isto é, que $\beta_1 > 0$ e $\beta_2 < 0$ , gerando uma parábola com concavidade para baixo, como na seguinte imagem:

No entanto, existe uma outra especificação para identificar a Curva de Kuznets, gerando também aos dados fitados uma parábola com concavidade para baixo, ou seja, uma relação de u invertido. No caso, seria a seguinte:

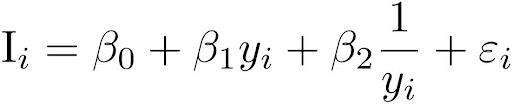
Nesta especificação, se $\beta_0 < 0, \beta_1 < 0, \beta_2 < 0$ , daí teríamos a relação desejada. Para entender porquê, tomemos essa especificação como a soma das seguintes funções:

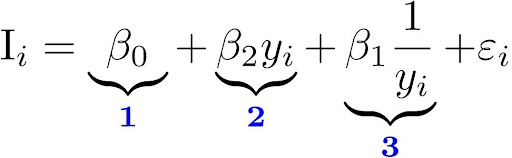
Que produz o seguinte gráfico:

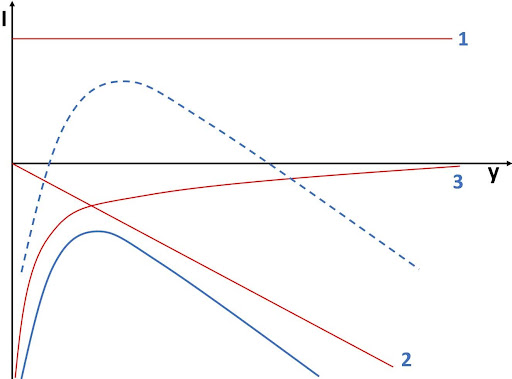
A primeira função é descrita por $\beta_0$ , que é uma constante positiva, por isso representada como uma linha horizontal acima de zero. A segunda função é descrita por $\beta_1y$ , que nada mais é que uma função afim linear negativa. Já a terceira função é descrita por $\beta_2\frac{1}{y}$ , que tende a $-\infty$ quando y se aproxima de zero e tende a zero quando y tende ao infinito.

A soma horizontal das funções 2 e 3 forma uma parábola com concavidade para baixo, só que para valores abaixo de zero, pois ela começa assintoticamente da função 3 e converge assintoticamente para a função 2. Essa curva está representada pela linha azul cheia. Ao fazer a somar horizontal com a função 1, se a constante $\beta_0$ for suficientemente alta, então geramos a curva com formato de u invertido, passando por valores positivos, como desejávamos.

Além disso, há uma outra forma importante de estimação da Curva que é o uso de dados em painel. Conseguimos observar por múltiplos períodos de tempo dados de vários países diferentes, assim gerando uma sequência temporal de cortes transversais de vários países.

Qual é a vantagem de dados em painel? O fato de podermos eliminar algumas variáveis confundidoras na relação que buscamos estimar. Quais variáveis? Aquelas que são fixas ao longo do tempo. A intuição é que há uma possível confusão por uma variável que está mediando o efeito que queremos estimar, mas como estamos olhando a variação no tempo e supondo que tal variável não se altera, então podemos eliminar o seu efeito.

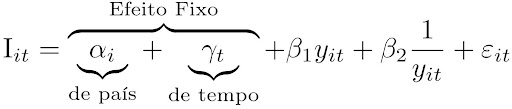
*Nesse exemplo estamos adotando a última especificação.*

A vantagem da especificação em dados em painel pode ser observada na imagem abaixo. Nela, cada curva representa a trajetória de Kuznets de um país específico ao longo do tempo. O país 1 possui a curva de Kuznets mais deslocada para cima, ao passo que o país 3 tem a curva de Kuznets mais abaixo, enquanto o país 2 está em uma posição intermediária.

Imagine que há dados de vários países e cada país tem sua trajetória de Kuznets diferente. Ou seja, qualitativamente a relação entre desigualdade e renda de um país é dada por um u invertido, mas em cada país essa trajetória é única. Portanto, cada país tem sua trajetória deslocada por um fator de escala que é graficamente capturado pela adição do efeito fixo de país $\alpha_i$ que representamos na especificação acima. Assim, o efeito fixo de país serve como um “deslocador” da desigualdade para cada país. Dessa forma, tem-se que $\alpha_1 > \alpha_2 > \alpha_3$ .

Então, suponha que peguemos um corte seccional (cross section) de países, ou seja, observamos os países em apenas um momento do tempo. Podemos (potencialmente) observar que um país está no ponto marcado na trajetória 3 da imagem, enquanto tem-se outro país no ponto marcado da trajetória 2, e, por fim, um último país no ponto marcado da trajetória 1. Se estimarmos a relação com os dados configurados na forma descrita acima por Mínimos Quadrados Ordinários (MQO ou OLS), a regressão estimada indicaria que a relação entre renda e desiguldade é positiva, i.e., conforme aumenta-se a renda de um país, maior será sua desigualdade, como na imagem abaixo.

Mas se colocarmos um fator de escala de efeito fixo que corrige a diferença de interceptos entre os países, esse efeito vai fazer com que cada um deles tenha sua curva de Kuznets própria. Isto é, o país 1 terá o intercepto $\alpha_1$ , o país 2 terá o intercepto $\alpha_2$ e assim por diante. Isso faz com que seja possível capturar a relação de u invertido.

Em resumo, quando se usa um estimador de efeito fixo usando dados em painel, pode-se observar o u invertido; já se forem usados estimadores de MQO em dados cross section, não se observa o u invertido. Ou seja, concluímos que há uma clara vantagem em estimações usando dados em painel.

Verificação empírica da Curva de Kuznets (Parte 2)

Ahluwalia (1976)

Feitas essas adições analíticas, podemos nos voltar novamente à questão da verificação empírica da Curva de Kuznets. Olhemos para trabalhos que tentaram efetivamente estimar a Curva de Kuznets via dados em painel. Ahluwalia (1976, p. 311) fez isso utilizando uma especificação quadrática.

Na imagem abaixo, cada linha representa uma regressão com as mesmas variáveis independentes (dadas pelas colunas), mas com uma variável dependente diferente umas das outras. A variável dependente é o percentual da renda total que vai para os x% mais ricos/pobres da população. O que varia em cada variável dependente é o valor de “x”. A 1ª linha considera como variável dependente o percentual da renda total que vai para os 20% mais ricos do país; a 2ª, os 40% mais ricos; a 3ª, os 60% mais pobres; a 4ª, os 40% mais pobres; por fim, a 5ª coluna representa o percentual da renda total que vai para os 20% mais pobres do país.

A seção A são os resultados das regressões quando se considera a amostra completa, ao passo que a seção B filtra para apenas os países em desenvolvimento.

A 1ª coluna representa o valor da constante, i.e., o $\beta_0$ ; a 2ª ( $\beta_1$ ) é o coeficiente associado à variável log do PIB per capita dos países; a 3ª ( $\beta_2$ ) representa o coeficiente do quadrado do log do PIB per capita dos países. Por fim, a última coluna denota uma dummy de países socialistas.

A Curva de Kuznets diz que o percentual da renda agregada que vai para os mais ricos inicialmente aumenta e posteriormente diminui à medida que o país enriquece (o que equivale a dizer que a desigualdade do país inicialmente aumenta e depois diminui). Sendo assim, esperamos encontrar $\beta_2 < 0$ para os coeficientes estimados da regressão com o “Top 20 percent” (e talvez também o “Middle 40 percent“) como variável dependente.

Da mesma forma, a Curva de Kuznets diz que o percentual da renda agregada que vai para os mais pobres inicialmente diminui e posteriormente aumenta à medida que o país enriquece (o que, novamente, equivale a dizer que a desigualdade do país inicialmente aumenta e depois diminui). Sendo assim, esperamos encontrar $\beta_2 > 0$ para os coeficientes estimados da regressão com o “Lowest 20 percent” (e talvez também o “Lowest 40 percent“) como variável dependente.

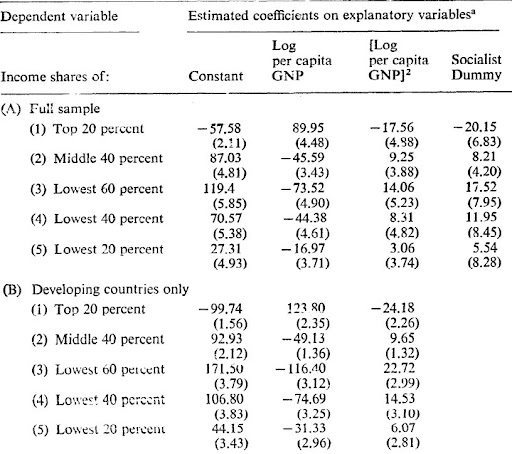
Na seção A e B, como era de se esperar, encontra-se $\beta_2 < 0$ quando olhamos para os percentuais mais ricos da população e $\beta_2 > 0$ quando olhamos para os percentuais mais pobres. Ou seja, quando olhamos para uma amostra grande de países, a relação prevista pela teoria se mantém.

A figura abaixo ilustra os resultados das regressões. Nela, tem-se a linha de regressão considerando a fatia da renda agregada que vai para os 40% mais pobres da população. A Curva de Kuznets diz que o percentual da renda agregada que vai para os mais pobres inicialmente diminui e posteriormente aumenta à medida que o país enriquece (o que equivale a dizer que a desigualdade do país inicialmente aumenta e depois diminui). Portanto, espera-se que a linha de regressão em questão tenha um formato de ‘u’, e é exatamente isso que é observado.

Deininger & Squire (1998)

Vamos, por fim, apresentar uma estimativa mais moderna, proveniente de Deininger & Squire (1998), na qual foi feita usando a especificação consistindo na soma de três funções.

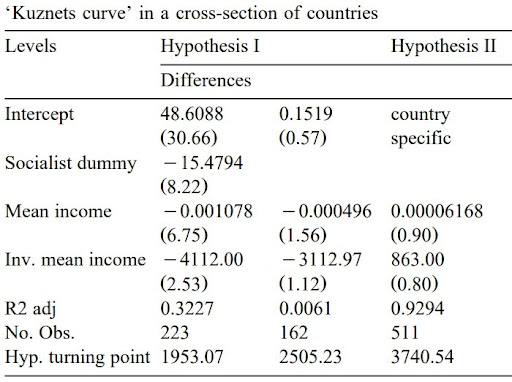
A figura abaixo mostra os resultados das regressões. Na hipótese I foram usados dados cross-section, enquanto que na hipótese II foram usados dados em painel. Outra diferença na estimação das hipóteses é que na II acrescenta-se de maneira exclusiva uma dummy de país para aumentar a comparabilidade entre as observações na amostra, enquanto na primeira hipótese acrescenta-se de maneira exclusiva uma dummy de países socialistas, tal como foi feito nas últimas regressões que observamos.

A variável dependente é o índice GINI do país. “Mean income” representa a renda média do país; ao passo que “Inv. mean income” representa o inverso da renda. Vamos chamar os coeficientes associados a essas variáveis de, respectivamente, $\beta_1$ e $\beta_2$ .

Dada a teoria, deveríamos observar $\beta_2 < 0$ . Na especificação sem intercepto de país (hipótese I), encontra-se de fato $\beta_2 < 0$ , e isso tanto com a dummy de país socialista quanto sem. Ou seja, o resultado está de acordo com o esperado pela teoria. Agora, quando consideramos os efeitos fixos de país (hipótese II), controlando pelo nível de desigualdade dos países, não se encontra a relação desejada, pois $\beta_2$ é positivo e estatisticamente significativo. Portanto, quando estimamos a relação usando efeitos fixos, consequentemente usando uma técnica mais sofisticada e que supostamente ajudaria a encontrar de maneira melhor a relação, justamente não a encontramos. Os valores estimados não são consistentes com o que era esperado pela teoria.

A ideia de apresentar essas evidências da Curva de Kuznets é justamente demonstrar a dificuldade empírica de fazer essa documentação de forma correta. Como queremos fazer uma inferência da trajetória individual da renda de cada país, na ausência de dados em um horizonte de tempo longo o suficiente, temos de recorrer a inferências com base em corte transversal de países, o que nos compromete a uma hipótese forte de que um país representa o contrafactual do outro. Quando consideramos o efeito fixo de países utilizando uma especificação mais moderna, tem-se resultados não consistentes com a teoria.

Dessa forma, cabe a seguinte indagação: seria essa relação supostamente estrutural de fato uma relação estrutural? Os problemas encontrados derivam apenas da dificuldade de documentar tal relação empírica devido a uma insuficiência de dados para fazer uma inferência crível ou seria apenas o caso de que a relação é espúria, decorrente da sensibilidade dos resultados à especificação econométrica e o modelo usado? Nesse caso, qual seria a variável confundidora que está gerando o resultado enviesado? Qual é a relação de fato entre desigualdade e crescimento econômico? Fica a pergunta no ar.

Conclusão

A discussão sobre desigualdade e crescimento é importante e continua até os dias de hoje, sendo retomada nos últimos tempos após o lançamento do livro “O Capital no século XXI” (2013) do economista Thomas Piketty, em que o autor faz um trabalho muito cuidadoso com base de dados inéditas olhando para impostos de renda e outras fontes, mostrando que essa reversão do nível de desigualdade previsto pela curva de Kuznets para níveis de rendas mais altos não acontece. Entretanto, uma série de autores têm contestado as evidências apresentadas por Piketty, como Acemoglu & Robinson (2015), Geloso et al. (2022), Góes (2016) e Mankiw (2015).

Ou seja, essa é uma discussão em andamento na literatura e está longe de um consenso. Então a pergunta persiste: há uma relação estrutural entre desigualdade e crescimento? Quais são os mecanismos teóricos pelos quais uma relação dessa poderia vir a emergir?

Antes de tudo, é preciso ter cautela com a naturalização da desigualdade em virtude de certo objetivo, como por exemplo, crescimento econômico. Com o presente texto, demonstramos que tal fato estilizado está longe de ser consensual na literatura, além de sua documentação se basear em hipóteses muito fortes. Assim, esperamos um debate mais qualificado e consciente da teoria econômica e das evidências.

Referências

Acemoglu, Daron, & James A. Robinson. “The rise and decline of general laws of capitalism.” Journal of economic perspectives 29.1 (2015): 3-28.

Ahluwalia, Montek S. “Inequality, poverty and development.” Journal of development economics 3.4 (1976): 307-342.

Deininger, Klaus, & Lyn Squire. “New ways of looking at old issues: inequality and growth.” Journal of development economics 57.2 (1998): 259-287.

Geloso, Vincent J., et al. “How pronounced is the U-curve? Revisiting income inequality in the United States, 1917–60.” The Economic Journal 132.647 (2022): 2366-2391.

Góes, Carlos. Testing Piketty’s hypothesis on the drivers of income inequality: evidence from panel VARs with heterogeneous dynamics. International Monetary Fund, 2016.

Kuznets, Simon. Economic Growth and Income Inequality. American Economic Review 45 (1955): 1–28.

Mankiw, N. Gregory. “Yes, r> g. So what?.” American Economic Review 105.5 (2015): 43-47.

Piketty, Thomas. “Capital in the 21st Century.” Cambridge, MA: President and Fellows, Harvard College (2013).

Ray, Debraj. Development economics. Princeton University Press, 1998.