Depois de já termos exposto a intuição e a álgebra por trás do cálculo diferencial na primeira parte desta série, agora iremos nos debruçar sobre a aplicação dessa ferramenta na economia.
3. A aplicação do cálculo diferencial na ciência econômica
Como abordado no texto anterior, o cálculo diferencial é considerado uma das maiores inovações matemáticas da história. Entender o significado por trás da sua aplicação é uma peça fundamental para compreender os procedimentos de formalização matemática na ciência econômica. Esta parte do texto será composta com explicações de 3 áreas da Economia em que a sua aplicação é importante.
Para avançar nesta parte, é preciso desenvolver um pouco mais o raciocínio de cálculo diferencial. Até o momento, abordamos casos de funções com apenas uma variável. Mas, na Ciência Econômica, a grande maioria dos modelos estudados são funções que possuem pelo menos duas variáveis.
Por exemplo, uma função muito usada em modelagem microeconômica é a Cobb-Douglas, que é algebricamente representada da seguinte forma:

Do ponto de vista geométrico, a principal diferença entre uma função de uma variável para uma de duas variáveis é a representação gráfica. Funções de uma variável são graficamente representadas em um plano de duas dimensões, já de duas variáveis, em um plano de três dimensões. Uma representação gráfica da função Cobb-Douglas é a seguinte:
Agora considerando a parte operacional, como — em geral — não estamos interessados na variação total da função, mas sim considerando a mudança de uma variável mantendo as outras constantes, então derivamos uma variável de cada vez. Este procedimento se chama derivada parcial de f em relação x, em que x representa a variável considerada.
Pela definição de derivada parcial através do limite, temos:

De modo que, se o limite existir, somente a variável muda, e as outras são tratadas como constantes.
Por exemplo, derivando parcialmente em relação a x a seguinte função:

Pela definição de derivada:

Multiplicando pelo conjugado:


A derivada parcial de f em relação a x, seja usando as regras de derivação ou a definição de derivada pelo limite, é dada pelo resultado acima. O seu significado matemático é que, dado uma variação de x — ceteris paribus —, f irá variar conforme o resultado da derivada. O significado econômico — considerando uma função de utilidade — é o quanto o meu bem-estar aumenta, dado uma variação de “x” com “y” constante; ou seja, a utilidade marginal do bem.
Agora que entendemos como funciona o processo de derivada parcial, podemos aplicá-la em várias áreas da Ciência Econômica.
3.1. Cálculo diferencial em microeconomia
Um dos assuntos clássicos da microeconomia é solucionar o problema do consumidor. Dada uma função de utilidade U(x,y) = x^{\alpha}y^{1-\alpha}, sujeita a uma restrição orçamentária px + py = m, qual a quantidade demandada dos bens que maximiza a utilidade do agente representado?
Este assunto já foi tratado de maneira brilhante nesse texto do Gabriel Ferraz, portanto não me estenderei muito no assunto, apenas me restringirei à parte operacional de um problema específico.
Exemplo com Cobb-Douglas:
O problema do consumidor para uma função de utilidade no caso de dois bens é:

Para resolver o problema, montamos o seguinte Langrageano:

As condições de primeira ordem (CPO) desse problema resultam em:

Perceba que as derivadas estão sempre igualadas a zero. Ou seja, lembrando da explicação dada na seção de cálculo diferencial, buscamos o ponto crítico de cada variável. Do ponto de vista econômico, encontramos a utilidade marginal do bem, ou seja, o quanto de acréscimo de uma unidade de um bem aumenta o grau de bem-estar do agente econômico, ceteris paribus.
Dividindo a primeira CPO pela segunda, obtemos:

Na primeira equação acima, temos a igualdade entre o valor absoluto da Taxa Marginal de Substituição (TMS) — o significado econômico é o quanto estou disposto a sacrificar de um bem para adquirir uma unidade a mais de outro bem, de modo a deixar indiferente o meu bem-estar — e a relação de preços entre os bens x e y. Desse modo, temos a condição que possibilita a otimização entre a curva de indiferença e a reta orçamentária.
Substituindo a expressão de y acima na reta orçamentária, temos:

Substituindo o valor de x na expressão de y:
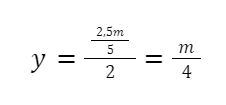
Desse modo, as demandas ótimas para os bens x e y são:

Se considerarmos que a renda seja m = 134, temos que as demandas ótimas são:

que proporcionam a seguinte utilidade:

Graficamente, a representação seria da seguinte maneira:
3.2. Cálculo diferencial em macroeconomia
Quando estudamos macroeconomia, um dos primeiros modelos abordados é o modelo da curva IS. A curva IS é o modelo macroeconômico, de curto prazo, que representa o lado da demanda por bens de uma determinada economia. Este modelo capta como uma mudança nas decisões de gastos das famílias, firmas e governos afetam o produto da economia. A curva IS relaciona combinações de taxas de juro com o produto, de modo que a economia permaneça em equilíbrio — ou seja, quando a despesa é igual à produção.
Uma aplicação intuitiva e prática do Cálculo Diferencial é através do cálculo do multiplicador de gastos do governo. Sabemos que um dos componentes da identidade do PIB é o consumo das famílias, de modo que é razoável supor que uma parte da renda é destinada para consumo e outra para poupança. O modelo keynesiano de consumo incorpora esta suposição:

em que “C” é o consumo agregado, “C_0” é o consumo que independe da renda, “C_1” é a proporção da renda disponível direcionado ao consumo, “t” é a proporção do imposto e “y” é a renda das famílias.
De acordo com esta teoria de consumo, as famílias não transformam totalmente a sua renda em bens e serviços, de modo que parte dela é poupada.
Quando colocamos a equação de demanda agregada, que incorpora a modelagem de comportamento do consumo agregado, no diagrama de equilíbrio do mercado de bens, temos:

em que “Y_D”, devido à parte de consumo autônomo “C_0”, não parte do ponto 0 do diagrama, e devido a “C_1(1-t)” a inclinação é inferior a 1. O ponto de encontro entre as duas retas representa o nível de produto “Y_D” que se encontra no equilíbrio no mercado de bens e serviços.
Dado “C_1(1-t)”, é possível encontrar o efeito multiplicador dado uma variação nos gastos do governo “G”. A intuição por trás é que um aumento dos gastos do governo provoca uma diminuição no nível de desemprego — o que aumenta a renda da economia e a necessidade de produção; as firmas, para suprir a demanda, contratam mais trabalhadores, que aumenta a renda e a demanda, e o ciclo se repete. Porém, como nem toda renda é consumida, o efeito multiplicador é finito. O raciocínio pode ser representado graficamente da seguinte maneira:

De forma algébrica, sem modelar I, temos:

Colocando “Y” em evidência:

Supondo um aumento de “G”, sendo e “t = 0,4”, ou seja “1 - C_1(1-t) = 0,52”. Se quisermos encontrar o efeito multiplicador dada uma variação nos gastos do governo “G”, usando a definição de derivada pelo limite, basta:


Percebam que o multiplicador é o coeficiente angular de Y. Desse modo, um aumento de R$1,00 nos gastos do governo aumenta a produção em R$1,92.
Para observar o efeito multiplicador geometricamente, tendo a primeira equação de demanda agregada com apenas o modelo de consumo:

3.3. Cálculo diferencial em econometria
O modelo econométrico básico, que é estudado em todos os cursos de Econometria, é a regressão linear simples (RLS). De maneira geral, considerando uma quantidade de dados, a RLS estima parâmetros para uma equação de reta, de modo a relacionar o comportamento de duas variáveis “x” e “y”, na tentativa de explicar “y” nos termos de “x”. Ou seja, a RLS é uma ferramenta de análise estatística que mensura o grau de influência de uma variável “x” sobre uma variável “y”, através do efeito de uma variação de “x” sobre a variação de “y”, mantendo outros fatores constantes.
Em termos algébricos:

Porém, dificilmente são encontrados dois aspectos que se relacionam um a um na natureza. Ou seja, ao menos na RLS, o que não foi explicado pela variável “x” estará no termo de erro “u”. Os parâmetros da RLS são estimados assumindo algumas hipóteses, dentre elas a de que a soma dos quadrados dos resíduos — ou seja, a soma dos quadrados das diferenças entre o valor real e o valor estimado — seja a menor possível. Desse modo, temos um problema de minimização.
Algebricamente:

As condições de primeira ordem (CPO) desse problema resultam em:

O -2 foi desconsiderado por se tratar de uma constante. Ou seja, seria eliminado por manipulação algébrica.
Isolando \beta_1 na primeira equação e dividindo por n:

Percebam que o quociente entre a soma de variáveis pela quantidade de termos é a sua média.
Substituindo o resultado acima na segunda equação da CPO:

Manipulando através das propriedades de somatório:

Colocando o estimador \hat\beta_1 em evidência:

Isolando o estimador \hat\beta_1:

Ou seja, através do conhecimento de derivada e tomando algumas propriedades de somatório, conseguimos derivar as fórmulas dos estimadores de uma RLS que minimizam o somatório dos termos de erro ao quadrado.
(Na manipulação algébrica do problema acima, foram usadas as propriedades de somatórios dadas pelo Apêndice A do livro do Wooldridge)
4. Conclusão
Pudemos perceber ao longo do texto que o Cálculo Diferencial é uma ferramenta que tem grande aplicação na Ciência Econômica. Foram abordadas apenas algumas aplicações nas três grandes áreas da Economia: Microeconomia, Macroeconomia e Econometria. Entender a intuição por trás da derivação, na minha percepção, é o fundamento para realmente compreender a teoria econômica e perceber a beleza por trás do processo de formalização da Economia, como forma de amadurecimento desta ciência. A matemática é uma linguagem que, quando entendido as suas regras internas, possibilita grandes feitos.
Referências
GUIDORIZZI, Hamilton. Um curso de Cálculo. 5ª Ed. Rio de Janeiro: GEN/LTC.
EVES, Howard. Introdução à História da Matemática. 5ª Ed. São Paulo: Editora Unicamp.
PINDYCK, Robert S; RUBINFELD, Daniel. Microeconomia. 8. ed. São Paulo: MAKRON.
C. P. Simon, L. Blume. “Matemática para Economistas”, Ed. Bookman, 1ª. Edição, 2004.
POPPER, Karl R. A lógica da pesquisa científica. São Paulo: Editora Cultrix, v. 1, 2008.
WOOLDRIDGE, J. M. Introdução à econometria: Uma abordagem moderna. São Paulo: Thomson, 2005.
.
Leia também:
O cálculo diferencial e sua aplicação na economia (Parte 1)
Projeto Matemática – Apresentação
Correlação não é causalidade. Mas por quê?
Fundamentos 02 – Lógica










Deixe um comentário