Um cientista, seja teórico ou experimental, formula enunciados ou sistemas de enunciados e verifica-os um a um. No campo das ciências empíricas, para particularizar, ele formula hipóteses ou sistemas de teorias, e submete-os a teste, confrontando-os com a experiência, através de recursos de observação e experimentação.
– POPPER, Karl; A Lógica da Pesquisa Científica, p. 27
1. A importância metodológica da Matemática para a Ciência Econômica
A formalização matemática da Economia, devido não só à precisão e economicidade lógica que esta linguagem possui, mas também à possibilidade de estabelecer e extrair informações quantitativas a respeito da relação entre duas ou mais variáveis, é tida por muitos como um dos grandes saltos no processo de amadurecimento da ciência econômica como área do saber científico, no sentido moderno do termo. Ou seja, a matematização de uma ciência permite não só observar se há correlação entre duas ou mais variáveis “X“, “Y ” ou “Z“, mas também o quanto de uma variação de “X” explica uma variação de “Y” ou “Z”.
A linguagem matemática estabelece a precisão lógica, de modo a evitar vieses e vícios de raciocínios a que outras formas de linguagem estão sujeitas, e economicidade argumentativa, de maneira a reduzir um argumento de várias páginas em uma simples dedução algébrica. Estas características proporcionam grande importância metodológica ao estudo da Ciência Econômica — e, também, a outros ramos das ciências.
Dentro do entendimento do que é considerado científico na concepção moderna da Filosofia da Ciência, ou seja, tomando o falseabilismo popperiano como critério de demarcação entre enunciados científicos e pseudocientíficos, de modo que a qualidade científica está na possibilidade de uma teoria ser contraditada pela experiência, a precisão lógica da matemática é complementada pelo falseabilismo. Isto se dá pois a verificação de uma teoria, comparando-a com a realidade empírica, não necessariamente implica em sua validade. Ou seja, a validade lógica de um argumento não implica necessariamente em sua comprovação científica.
Por exemplo, considerando uma situação hipotética em que uma equação de demanda por maçãs é verificada em cada cidade de um estado brasileiro, é possível induzir que esta equação de demanda seja uma lei universal da demanda por maçãs? Obviamente que não. Ou seja, a mera verificação empírica de uma relação matemática não implica em uma comprovação científica ou absoluta. A cientificidade não deve estar em função da verificabilidade, mas da possibilidade de falseabilidade de um sistema.
Mas a matemática não é somente um conjunto de números e operações com vistas a determinar um valor numérico de uma equação, é um sistema lógico sofisticado que, sabendo de suas regras, possui a qualidade de facilitar o entendimento da abstração teórica — a que toda teoria está sujeita — e a quantificação do grau de influência entre variáveis, dada uma determinada função algébrica. Porém, para entender o significado econômico da aplicação matemática dentro da Ciência Econômica é preciso justamente entender os fundamentos que dão significado à própria área da matemática que está sendo operacionalizada pelo economista.
O objetivo deste texto é tentar fornecer este entendimento, se restringindo ao estudo do Cálculo Diferencial, e o significado econômico por trás da sua aplicação no estudo da Economia.
2. O que é o Cálculo Diferencial?
Em geral, quando estudamos conceitos matemáticos, a didática dos manuais e cursos se limita à operacionalização e aplicação do sistema que está sendo abordado, deixando um pouco de lado a sua origem histórica e o seu significado. De um certo ponto de vista, o enfoque na solução de problemas tem sua justificativa. A resolução intensiva de exercícios ajuda o aluno a internalizar os procedimentos próprios da área estudada. Porém, a falta de uma abordagem histórica provoca uma sensação de alienação e falta de propósito do porquê aquilo merece ser estudado. Estudar a origem dos conceitos matemáticos é uma forma de heurística que mantém a motivação do estudante.
Para evitar esse tipo de alienação — afinal, sensação pela qual eu mesmo experiencio —, iniciarei a explicação do Cálculo Diferencial a partir de sua origem histórica.
2.1. Uma breve contextualização histórica
Durante o século XVII, devido ao desenvolvimento de novas áreas de pesquisa e invenção de novas formas de interpretar os números, houve uma grande expansão do conhecimento na Matemática. No início do século, Napier revelou a sua invenção dos logaritmos, Harriot e Oughtred contribuíram para a álgebra, Galileu estabeleceu o paradigma da ciência dinâmica e Kepler fundamentou as leis que regem os movimentos dos planetas. Ainda nesse século, Descartes contribuiu com a geometria analítica moderna, Fermat com a teoria dos números e Huygens aprofundou a teoria de probabilidades.
Mas, considerado por muitos como a invenção mais importante e notável do período, a invenção do Cálculo veio mais ao final do século. O desenvolvimento do Cálculo é creditado principalmente a Isaac Newton e Gottfried Wilhelm Leibniz. Uma curiosidade a respeito do desenrolar histórico da criação do Cálculo é que, ao contrário de como muitos manuais ordenam o conteúdo, o Cálculo Integral surgiu antes do Cálculo Diferencial. A noção de integração teve origem em procedimentos de somatórios relacionados ao cálculo de determinadas áreas, volumes e comprimentos. Já a diferenciação, em período posterior, surgiu de problemas que envolviam tangentes e questões de máximos e mínimos.
Para melhor entender o processo histórico por parte da criação da disciplina de Cálculo, sugiro a leitura do livro “Introdução à história da Matemática”, de Howard Eves.
2.2. A noção intuitiva de diferenciação
Na minha percepção, entender a intuição gráfica por trás do Cálculo Diferencial é o ponto mais importante no processo de compreensão da disciplina, pois, se começarmos — como usualmente é feito — pela definição algébrica de limite, aumentamos em muito a complexidade, o que dificulta substancialmente o entendimento.
Como foi dito anteriormente, o desenvolvimento do cálculo diferencial surgiu de problemas que envolviam tangentes e pontos de mínimos e máximos de uma função. Buscando um significado prático, o ângulo da equação que representa a reta tangente ao ponto de uma função fornece informações muito úteis. Por exemplo, se descobrirmos a equação de uma reta que tangencia cada ponto de uma função, podemos obter a taxa de variação instantânea da função em um ponto; ou seja, a aceleração da função em um ponto. Na física, se considerarmos uma função de velocidade, temos a aceleração; na ciência econômica, assumindo uma função de produção, podemos encontrar a produtividade marginal dos fatores.
O gráfico abaixo mostra a dinâmica de uma equação de reta que tangencia todos os pontos de uma função:
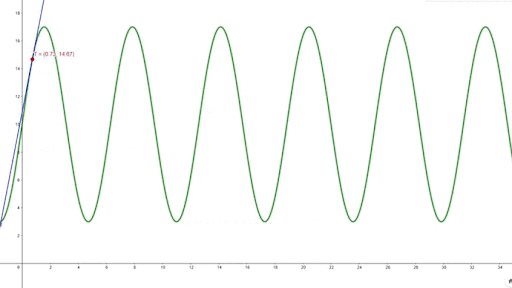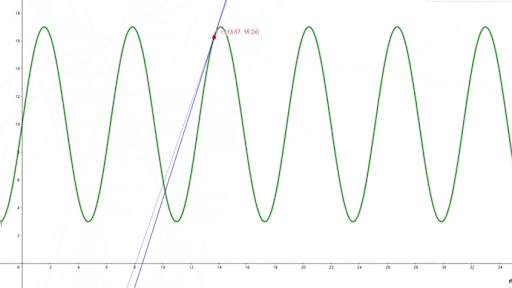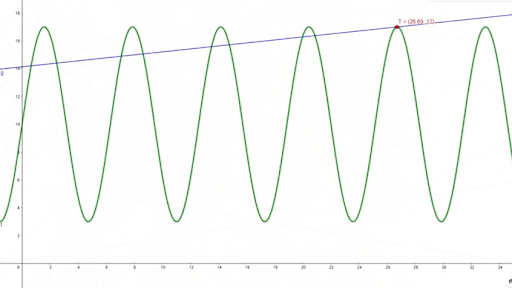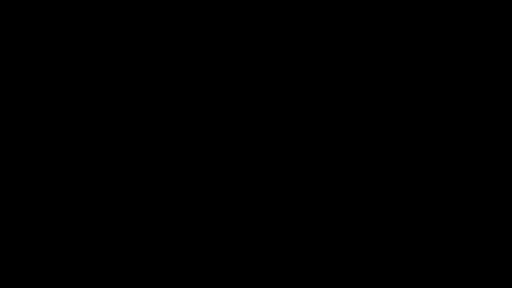
Como podemos observar, a angulação da reta se altera: de positivamente inclinada, acelerando; negativamente inclinada, desacelerando; e, quando a reta está nos pontos de mínimo e máximo da função, a angulação é igual a zero. Se a função do gráfico acima representa a velocidade de um veículo ao longo de uma via, de modo que o ponto de máximo é a velocidade máxima alcançada e o ponto de mínimo a velocidade mínima alcançada, podemos descobrir qual foi a aceleração do veículo em um determinado instante de tempo.
Então, vem a pergunta: como descobrimos o ângulo da reta tangente ao ponto?
2.3. Da intuição gráfica à construção algébrica
Para descobrirmos isso, precisamos antes definir o conceito de reta secante, ou seja, dado o gráfico de uma função, a reta será secante caso tenha dois ou mais pontos de interseção com a curva. Da seguinte maneira, sendo:
A = (A, f(A)); B = (B, f(B))
as coordenadas dos pontos.
Vamos supor que, dados os pontos A e B, queremos descobrir o quanto uma variação média de x implica uma variação média de f(x) . Para descobrirmos isso, precisamos construir um triângulo retângulo, de modo que as retas que o compõe são obtidas da seguinte forma:
Algebricamente:
\overline{AC} = \overline{CD} - \overline{AD} = \Delta X
e
\overline{BC} = \overline{BE} - \overline{CE} = \Delta Y
Sabemos da Geometria Analítica que o cálculo da tangente de um ângulo é:
Agora, o que acontece se deslocarmos o ponto “B” em direção ao ponto “A”? Observando o gráfico abaixo, percebemos que, quanto mais próximo “B” está de “A”, mais próxima a representação da reta secante se assemelha a uma reta tangente.
Ou seja, usando a notação geral, quanto mais próximox está de a, mais próximo estamos de encontrar o ângulo da reta tangente — ou a taxa de variação instantânea de um ponto. Contudo, o valor de x nunca poderá ser igual a a, pois isto implicaria uma divisão de zero por zero, o que sabemos que é indeterminado. Porém, se levarmos até o limite, teremos uma aproximação satisfatória da angulação da reta tangente.
De forma algébrica, temos:
Usando uma notação equivalente, em que h = x – a, temos:
Desta forma, a função derivada def(x) é definida como:
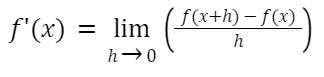
Desta fórmula básica conseguimos obter a derivada de qualquer função; e é dela que foi obtida as regras de derivação que estamos mais acostumados a utilizar. Por exemplo, dada a seguinte função:
Se aplicarmos a definição de derivada através do limite, temos:
Resolvendo o limite, temos:
2.4. Encontrando o ponto de máximo ou mínimo de uma função
Primeiro entendemos a parte intuitiva do cálculo diferencial, depois desenvolvemos a parte algébrica que fundamenta o cálculo do ângulo da reta tangente. Mas como descobrimos os pontos máximos e mínimos — algo fundamental para a otimização de funções sujeitas a restrições — de uma função?
Foi dito anteriormente que os pontos de máximos e mínimos de uma função são encontrados quando o coeficiente angular da reta tangente ao ponto for igual a zero. Ou seja, basta igualarmos a função derivada a zero e encontrar o valor do x correspondente.
Utilizando a função do exemplo anterior, temos, algebricamente:
Agora, desenvolvendo graficamente:
Ou seja, quando x = –1 na função derivada, encontramos f’(-1) = 0, que é o ponto crítico da função; que, com o auxílio do gráfico e pela concavidade definida no sinal do coeficiente angular de f(x), podemos afirmar que é um ponto de mínimo local.
Contudo, nem sempre temos um recurso gráfico ou uma função de fácil interpretação para nos ajudar. Então como determinar se o ponto crítico é um ponto de mínimo ou máximo local? A solução mais fácil seria calcular a taxa de variação instantânea dos pontos próximos ao ponto crítico, de modo que, se a derivada no ponto anterior for negativa e a derivada no ponto posterior for positiva, sabemos que neste ponto crítico a concavidade é virada para cima e, portanto, é um ponto de mínimo local da função.
Em caso qualquer, de uma função com a concavidade voltada para baixo, temos:
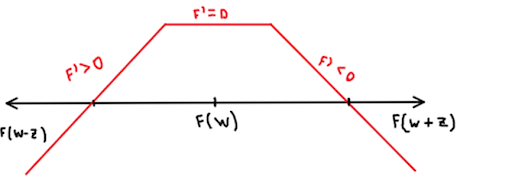
Para casos mais complexos, sugiro a abordagem dada pelo livro “Um Curso de Cálculo – Vol.1”, de Hamilton Luiz Guidorizzi.
Outra forma de verificar a concavidade de uma função é através do cálculo da segunda derivada. Ou seja, dada a função f’(x), o cálculo de f’’(x) trará a informação de se a taxa de variação no ponto está crescendo ou decrescendo, de modo que se f’’(x)>0, então a primeira derivada é crescente ao longo do tempo, logo a concavidade é voltada para cima; se f’’(x)<0, a primeira derivada é decrescente ao longo do tempo, então a concavidade é voltada para baixo.
De um ponto de vista gráfico:
Até o momento desenvolvemos as noções e aplicações básicas do cálculo diferencial. Na parte 2 iremos tratar a aplicação da derivada em problemas de ordem econômica e o significado por trás de cada aplicação abordada.
Deixe um comentário