Imagine o seguinte cenário apresentado por A. W. Tucker nos anos 40: duas pessoas foram responsáveis por um roubo bem sucedido. Depois de um tempo e de muita investigação policial, esses indivíduos são capturados pelas autoridades, que, apesar de incertas sobre o paradeiro dos assaltantes, estão sedentas por uma confissão. Para extraí-la, os oficiais, depois de segregar os suspeitos, os submetem a uma situação pela qual cada um deve escolher entre delatar o companheiro ou uma pena mais longa.
Em resumo, se o suspeito delatar o companheiro e não for delatado, lhe é prometida uma sentença de um ano, enquanto, a seu companheiro, é imposta uma pena quatro vezes maior. Se ambos confessarem, cada um recebe uma sentença de três anos. No entanto, os dois suspeitos sabem que, se ninguém confessar, serão sentenciados por um crime de menor importância – o que resultará numa pena de dois anos.
O cenário apresentado é o famoso dilema dos prisioneiros e é um exemplo de uma situação onde ambos os participantes têm de agir de maneira estratégica, ou seja, a ação de um depende do movimento do outro. A matemática aplicada e a economia têm desenvolvido um poderoso ferramental para estudar as ações individuais quando embutidas em um cenário estratégico: a teoria dos jogos.
Um jogo é um modelo abstrato de uma situação estratégica. Os jogos têm três elementos essenciais: (i) os jogadores, isto é, os tomadores de decisões no jogo, que são caracterizados por possuírem a habilidade de escolher entre um conjunto de ações possíveis; (ii) as estratégias, isto é, um conjunto de regras de procedimento a ser adotado em cada situação possível de ocorrer durante um processo decisório; e (iii) os payoffs, que são o retorno final dos jogadores na conclusão de um jogo, sendo mensurado em níveis de utilidade obtidos por eles próprios.
Então, em um nível mais geral, os elementos de um jogo são:
Número de jogadores;
Descrição das ações dos jogadores;
Descrição das estratégias dos jogadores;
Grau de informação dos jogadores;
Regras:
Horizonte de tempo/rodadas;
Informação;
O que é permitido ser feito;
Payoff.
No caso do dilema dos prisioneiros há 22 = 4 combinações de estratégias e dois payoffs para especificar para cada combinação. Então, ao invés de listar os payoffs, fica mais organizado e limpo representá-los na sua forma matricial.
Para entendermos o resultado desse jogo é preciso entendermos o conceito de equilíbrio de Nash. Dizemos que as estratégias escolhidas pelos jogadores constituem umequilíbrio de Nash se a estratégia escolhida por cada jogador for a melhor resposta das estratégias escolhidas pelos demais. Ou seja, nenhum jogador deseja mudar seu comportamento. Para avançarmos nas definições precisamos de algumas notações: Si denota o conjunto de estratégias do jogador i, sendo uma particular estratégia representada por si ∊ Si para o jogador i.
Definição: melhor resposta.
si é a melhor resposta para o jogador i às estratégias rivais s-i, denotada por si ∊ BRi(s-i), se: ui(si,s-i) ≥ ui(s’i,s-i) para todo s’i ∊ Si.
Definição: equilíbrio de Nash.
O equilíbrio de Nash é o perfil de estratégia (s*1, s*2, …., s*n) tal que para cada jogador i = 1, 2, …, n, s*n é a melhor resposta para a estratégia de equilíbrio do outro jogador s*-i. Isto é, s*i ∊ BRi(s*-i).
Na prática, o que isso quer dizer? Vamos voltar ao nosso jogo dos prisioneiros. O equilíbrio de Nash funciona assim: se o jogador coluna escolher delatar, a melhor resposta do jogador linha é delatar também, uma vez que este prefere ficar 3 anos preso a 4. Se o jogador coluna jogar silêncio, isto é, não delatar, então a melhor resposta do jogador linha ainda é delatar, uma vez que prefere ficar um ano preso a dois. Como o jogo é simétrico, o jogador coluna vai ter o mesmo raciocínio! Então ficamos com a seguinte representação visual:
Dadas as melhores respostas dos jogadores, o equilíbrio de Nash corresponde à confissão mútua, ou seja, a delação dos dois players, mesmo quando a situação de maior eficiência para ambos é claramente aquela em que ambos ficam em silêncio. Esse resultado aparentemente paradoxal não deriva do fato dos agentes serem estúpidos ou algo do gênero, muito pelo contrário, é consequência da interação estratégica de ambos.
A batalha dos sexos
Outro exemplo de jogo é a batalha dos sexos, um tipo de jogo que envolve estratégias puras (isto é, realizadas com 100% de certeza) e estratégias mistas (isto é, realizadas com algum grau de incerteza). A premissa desse jogo é que uma esposa (jogador linha) e um marido (jogador coluna) gostariam de sair para se divertir à noite. Eles podem ou ir a uma apresentação de teatro ou ver um jogo de futebol no estádio. Ambos preferem ficar juntos. Entretanto, a mulher prefere o teatro, ao passo que o homem prefere o futebol. Assim, a matriz de payoffs fica da seguinte maneira:
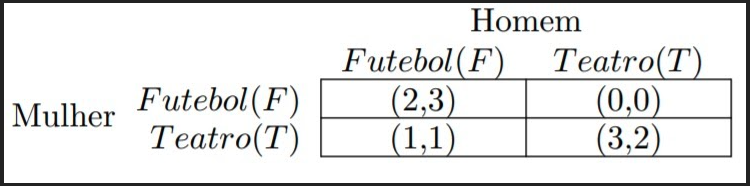
Em obediência ao que vimos até aqui, temos que a matriz congrega mais de um equilíbrio de Nash! Uma vez a mulher escolhendo ir ao teatro, a melhor resposta do marido é teatro. Se o marido escolher futebol, a melhor resposta da mulher é futebol também! Sendo assim, chegamos aos seguintes equilíbrios de Nash:
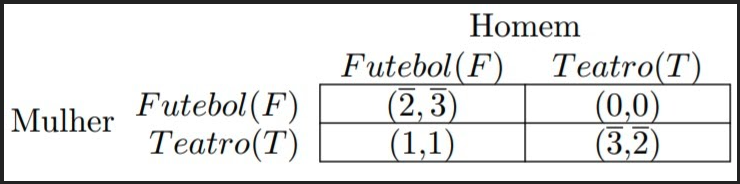
Em razão da sua simetria, esse jogo costuma dificultar a escolha de um resultado mais provável, sendo esse um exemplo de jogo sem estratégia dominantes, isto é, uma estratégia que retorna o pay-off mais alto independente da estratégia escolhida pelos demais jogadores. Para tornar as coisas ainda mais complicadas, temos mais um equilíbrio de Nash, que é aquele que resulta de estratégias mistas.
Como funciona a estratégia mista? Simples: o homem vai ao futebol com probabilidade PH(F) = q, enquanto vai ao teatro com probabilidade PH(T) = 1 – q. A mulher por sua vez vai ao futebol com probabilidade PM(F) = p, e vai ao teatro com probabilidade PM(T) = 1 – p. Disso se segue:
Decisão do homem: Quando o homem joga F? UH(F) = 3p + 1(1-p) e UH(T) = 0p + 2(1-p) Portanto, joga F se: UH(F) > UH(T) 3 + 1 – p > 2 – 2p 3p > 1 p > ¼
Decisão da mulher:
Quando a mulher joga F? UM(F) = 2q + 0(1-q) e UM(T) = 1q + 3(1-q) Portanto, joga F se: UM(F) > UM(T) 2q > q + 3 – 3q 4q > 3 q > ¾
Assim, chegamos no seguinte gráfico das funções de melhor resposta:
A função azul é a melhor resposta da mulher, enquanto a função verde é a melhor resposta do homem. Como podemos ver, as melhores respostas se encontram nos pontos (q = 0, p = 0), (q = 1, p = 1) e (q = ¾, p = ¼).
Jogos sequenciais
Até então, vimos apenas jogos simultâneos, ou seja, uma classe de jogos na qual os participantes tomam decisões ao mesmo tempo. Todavia, existe uma outra classe de jogos: os jogos sequenciais. Um exemplo clássico desse tipo de jogo foi a Guerra Fria, quando a decisão de jogar uma bomba sobre a nação adversária era contingente à decisão do que o outro país estava fazendo.
Se considerarmos a situação da Guerra Fria como um jogo simultâneo, estaríamos, mais ou menos, na seguinte situação. Os países (USA e URSS) tinham duas decisões: atacar ou não atacar. Se ambos atacassem, ambos sairiam prejudicados. Todavia, seria pior para o país que tivesse tomado a decisão de não atacar enquanto o adversário resolveu atacar. Nesse caso de jogo simultâneo, teríamos a seguinte matriz e equilíbrios de Nash:
Perceba que os equilíbrios de Nash nesse caso são ambos atacar ou ambos não atacar. Ocorre que o equilíbrio em que ambos atacam é inferior ao equilíbrio em que ambos não atacam, uma vez que o payoff no primeiro para cada participante é -10, enquanto que no segundo é 12. Como saberemos qual equilíbrio vai prevalecer? Para isso, precisamos estabelecer novos conceitos.
Como dissemos, esse é um jogo sequencial. Vamos tomar como o caso de que o primeiro a tomar uma decisão são os Estados Unidos. Logo, temos a seguinte árvore de decisão:
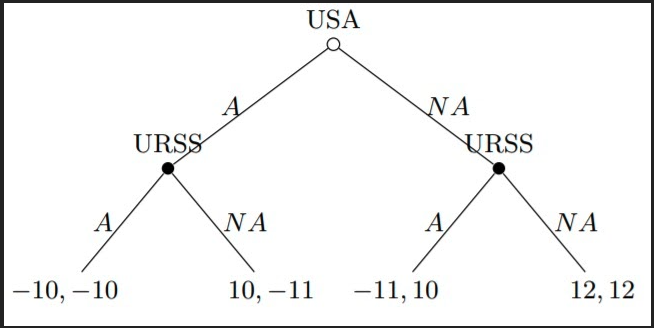
Os Estados Unidos começam o jogo tendo apenas um nó de decisão, enquanto a União Soviética tem dois nós. Tendo em vista esses nós, as estratégias (puras) são:
Ou seja, as estratégias da URSS são respectivamente: (A,A): atacar independentemente do que os Estados Unidos fizerem; (A, NA): Se USA atacarem, eu ataco; se não, não ataco; (NA,A): se USA atacarem, eu não ataco; se não atacarem, eu ataco; (NA,NA): independentemente do que USA fizerem, eu não ataco.
Ou seja, tendo visto as estratégias puras, a forma normal/matricial do jogo fica da seguinte forma (já considerando os equilíbrios de Nash):
Então qual vai ser o resultado do jogo? Qual é realmente a decisão que os países vão tomar, sendo que existem múltiplos equilíbrios? Para termos uma resposta, temos que entender um refinamento da noção do equilíbrio de Nash, que é o equilíbrio de Nash perfeito de sub-jogo.
Definição: equilíbrio de Nash perfeito de sub-jogo.
É um equilíbrio de Nash no qual as estratégias escolhidas não envolvem ameaças não críveis.
Para entender melhor, vamos considerar o nosso jogo. Se estou no primeiro nó, estou escolhendo entre -10 e -11. Claramente, minha melhor opção é atacar, pois isso vai me render -10, ao passo que não atacar vai me render -11. No segundo nó, a estratégia (NA, A) não é crível, uma vez que vai contra os interesses do tomador de decisão. Dessa forma, eliminando as ameaças não críveis, ficamos com o seguinte equilíbrio:
Para resolver o equilíbrio de Nash perfeito de sub-jogo, usamos um método chamado indução retroativa, que nada mais é do que começar do final, vendo as melhores decisões, até chegar no começo.
A lógica dessa indução seria, começando do final: se URSS estiver no primeiro nó, a jogada que maximiza seu payoff é atacar, pois -10 > -11. Agora, se a URSS estiver no segundo nó, a jogada que maximiza seu payoff é não atacar, pois 12 > 10. Consequentemente a ameaça (NA, A) e (NA, NA) não é crível. Logo, os USA estão escolhendo entre -10 e 12. No entanto, como 12 > -10, o equilíbrio de Nash perfeito de sub-jogo é aquele quando ambos não atacam. A URSS nunca permanecerá passiva quando é atacada, nem nunca vai atacar quando não é atacada.
Sendo assim, visualmente a resolução via indução retroativa fica:
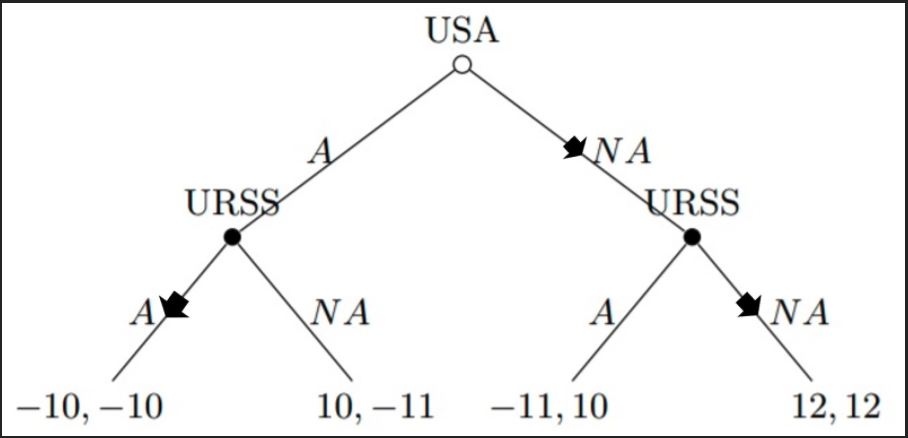
Conclusão
Esses jogos que apresentamos não esgotam o conteúdo de teoria de jogos, pois temos outros tipos de jogos, como os jogos repetidos, jogos bayesianos, além de desenho de mecanismo. Apresentamos apenas uma breve apresentação do conteúdo que se aprende na matéria de teoria dos jogos. Para saber mais, recomendamos o livro texto “Teoria dos Jogos”, de Ronaldo Fiani.
Deixe um comentário