“O modelo DSGE é simplesmente um modelo dinâmico, essa é a parte D. Leva em conta o tempo. […] E estocástico [essa é a parte S] porque há coisas inesperadas […], há coisas que são difíceis de prever, então modelamos como coisas estocásticas; e, finalmente, temos o Equilíbrio Geral [GE], que é a última parte do modelo DSGE, e significa que estamos levando em consideração o sistema como um todo. Não modelamos as partes individuais sozinhas, mas modelamos as partes como partes de um sistema geral e isso é essencial para entendermos como isso vai evoluir.” – Larry Christiano (link)
Introdução
Uma transformação ocorreu na macroeconomica na década de 70, cujos efeitos reverberam até hoje. Na esteira da Revolução das Expectativas Racionais e da crítica de Lucas, a chegada dos modelos de Ciclos Reais de Negócios (RBC) deslocou o mainstream da profissão (com algumas exceções) para longe das questões de heterogeneidade e agregação, típicas do debate macro da década anterior, em direção a questões relacionadas a dinâmica e expectativas (Baqaee & Farhi, 2018). Um desdobramento notável dessas transformações foi uma aparente derrocada do pensamento keynesiano, por parecer insuficiente para explicar os fenômenos macros, assim como as crescentes críticas dos economistas no campo Novo Clássico que, no debate macro, se firmaram metodologicamente. (Para ler mais sobre esse período, leia aqui).
Segundo Galí (2015, p. 2): “Do ponto de vista metodológico, a teoria RBC estabeleceu firmemente o uso de modelos dinâmicos estocásticos de equilíbrio geral (DSGE) como uma ferramenta central para a análise macroeconômica. As equações comportamentais que descrevem variáveis agregadas foram assim substituídas por condições de primeira ordem de problemas intertemporais enfrentados por consumidores e empresas. Suposições ad hoc sobre a formação de expectativas deram lugar a expectativas racionais”.
Entretanto, os modelos RBC sofriam de alguns problemas, pois assumiam que as flutuações cíclicas não sinalizavam necessariamente uma alocação ineficiente de recursos, dado que eram respostas ótimas dos agentes. Essa visão implicava que as políticas de estabilização não eram necessárias ou desejáveis, e poderiam até ser contraproducentes. Além disso, por focar em fatores reais, então naturalmente não havia espaço para discutir questões monetárias, de modo que essa modelagem teve um impacto muito limitado sobre os bancos centrais, uma vez que não era percebida como produzindo uma estrutura relevante para a análise de políticas- sendo que há uma ampla gama de evidências desde Friedman & Schwartz (1963) de que a política macroeconômica tinha capacidade de influenciar a evolução da produção e do emprego, pelo menos a curto prazo.
Além dos desafios empíricos mencionados acima, as implicações normativas dos modelos monetários clássicos também levaram muitos economistas a questionar sua relevância como uma estrutura para avaliação de políticas. O conflito entre as previsões teóricas e as evidências, e entre as implicações normativas e a prática política, pode ser visto como um sintoma de que alguns elementos que são importantes nas economias reais poderiam estar faltando nos modelos monetários clássicos. Essas deficiências são a principal motivação por trás da introdução de algumas suposições keynesianas, mantendo o aparato RBC como a estrutura subjacente. Os modelos novo-keynesianos adotam os seguintes elementos, como consta Galí (2015, p. 5-6):
- Competição monopolística. Os preços e/ou salários são fixados por agentes econômicos privados de forma a maximizar os seus objetivos, em vez de serem fixados por um leiloeiro walrasiano anônimo que procura desobstruir todos os mercados.
- Rigidez nominal. As empresas estão sujeitas a algumas restrições quanto à frequência com que podem ajustar os preços dos bens que vendem. Alternativamente, eles podem enfrentar alguns custos de ajuste desses preços. O mesmo tipo de atrito se aplica aos trabalhadores – ou aos sindicatos que os representam – na presença de salários rígidos.
- Não-neutralidade de curto prazo da política monetária. Como consequência da presença de rigidez nominal, mudanças nas taxas de juros nominais de curto prazo (quer sejam escolhidas diretamente pelo banco central ou induzidas por mudanças na oferta de moeda) não são compensadas por mudanças de um para um na inflação esperada, levando, assim, a variações nas taxas de juros reais. Estas últimas provocam mudanças no consumo e no investimento e, consequentemente, na produção e no emprego, uma vez que as empresas consideram ótimo ajustar a quantidade de bens ofertados ao novo nível de demanda. O mesmo vale para os trabalhadores na presença de salários rígidos. No longo prazo, porém, todos os preços e salários se ajustam e a economia volta ao seu equilíbrio natural, ou seja, o equilíbrio que prevalece na ausência de rigidez nominal. (Para saber mais leia aqui).
Antes de adentrarmos em uma versão do modelo Novo Keynesiano, vamos brevemente passar por sua história. Enquanto a literatura macro parecia dominada pelo campo das expectativas racionais e o domínio keynesiano sucumbindo, eis que surgem os trabalhos de Fischer (1977) e Phelps & Taylor (1977), trabalhos que, adotando as inovações teóricas no meio macro, conseguiram demonstrar que era possível preservar insights keynesianos clássicos como a rigidez dos preços e a relevância estabilizadora da política econômica.
Esses trabalhos pioneiros se desdobram em um novo programa de pesquisa de tentar microfundamentar os aspectos ad hoc macroeconômicos do modelo keynesiano que vigorava até então. Ou seja, diferente do campo novo clássico que partia da micro para chegar na macro, esse outro campo partia da macro e voltava na micro para dar solidez (Stiglitz & Greenwald, 1987). Entre esses empreendimentos podemos citar o conceito de salário eficiente desenvolvido por Shapiro & Stiglitz (1984) e o de custos de menu desenvolvido mais extensivamente por Mankiw (1985). Ambos servem para mostrar imperfeições e fricções no mercado que acarretam em flutuações no comportamento agregado. Assim, preservando a tese keynesiana de que a causa mais frequente do ciclo de negócios são flutuações na demanda agregada.
O desenvolvimento desse projeto de pesquisa não foi feito conscientemente guiado por uma vanguarda de pesquisadores que se comunicavam trilhando um fim específico e claro. Na verdade, foram trabalhos aleatórios e independentes que na literatura foram agregados no que ficou conhecido como a escola Novo Keynesiano. Essa escola nitidamente heterogênea desenvolveu vários modelos concorrentes ao modelo de Ciclo Real de Negócios, dentre os quais podemos citar o trabalho de Rotemberg (1982), Blanchard & Kiyotaki (1987), Rotemberg & Woodford (1997).
Hoje em dia, todos esses trabalhos de inspiração keynesiana foram agrupados e sintetizados no modelo básico Novo Keynesiano, que tornou-se um padrão na pós-graduação de economia, sendo um benchmark para desenvolver extensões e estudar macroeconomia. Os modelos de equilíbrio geral dinâmico e estocástico com acréscimo de elementos ao benchmark novo keynesiano é utilizado rotineiramente por bancos centrais do mundo todo, como por exemplo, no Stochastic Analytical Model with a Bayesian Approach (SAMBA) do Banco Central brasileiro (Castro et al. 2015), no New Area-Wide Model (NAWM) do Banco Central europeu (Christoffel et al. 2008), no Japanese Economic Model (JEM) do Banco Central japonês (Fujiwara et al. 2005), e assim por diante.
O resumo acima não esgota o assunto, então para saber mais leia Gordon (1990) e Galí (2018). Para estudar macro com a abordagem novo keynesiana com uso de DSGE de maneira acessível, leia Wickens (2012), enquanto para estudá-la de maneira mais rigorosa leia Galí (2015) e Costa (2018).
O modelo
Para apresentar o modelo, seguirei de perto o capítulo 3 do manual de Costa (2018). Para entendê-lo não é necessário saber programação dinâmica, entretanto é preciso saber o método de otimização por multiplicadores de Lagrange. Tal modelo é uma extensão do modelo RBC (que por tabela é uma extensão do modelo neoclássico de crescimento) que acrescenta as fricções no mercado essenciais para o pensamento keynesiano, uma vez que essas seriam o verdadeiro mecanismo gerador das flutuações na economia.
Em relação ao RBC, o modelo novo keynesiano básico preserva o comportamento das famílias. Entretanto, o problema da firma torna-se mais complexo, exigindo a inclusão de mais dois setores: firmas produtoras de bens finais (varejistas) e firmas produtoras de bens intermediários (atacadistas). A concorrência imperfeita, baseada no modelo de competição monopolística presente em Dixit & Stiglitz (1977), ocorre no setor atacadista, que produz bens diferenciados que são vendidos e agregados pelos varejistas em um ambiente de concorrência perfeita. Para relembrar os conceitos essenciais do modelo, leia aqui, aqui e aqui. Para uma versão de graduação (ainda mais) simplificada do modelo, leia aqui, aqui e aqui.
Famílias
As famílias utilizam o mesmo comportamento otimizador do modelo RBC, tomando que o indivíduo representativo possui uma função consumo agregado com a seguinte forma funcional:

onde \psi é a elasticidade de substituição entre esses bens diferenciados, possuindo grande significado econômico em modelos novo keynesianos, pois determina em que grau, do ponto de vista do consumidor, os produtos diferem uns dos outros. Em um extremo está o valor \psi \to \infty (\lim_{\psi \to \infty}\frac{\psi - 1}{\psi} = 1) , que, quando é substituído na expressão acima, resulta na soma linear simples c_{1} + c_{2} + c_{3} + \dots + c_{N} . Assim, cada bem de consumo é tão bom quanto qualquer outro, do ponto de vista do consumidor representativo, ou seja, os bens são substitutos perfeitos. Com \frac{\psi - 1}{\psi} > 1 , no entanto, os bens são apenas substitutos imperfeitos, o que significa que eles são diferenciados em algum grau, dependendo do valor exato de \psi . Geralmente, os modelos novo keynesianos assumem \frac{\psi - 1}{\psi} > 1 .
Dada essa função, as famílias otimizam a seguinte função utilidade CES:
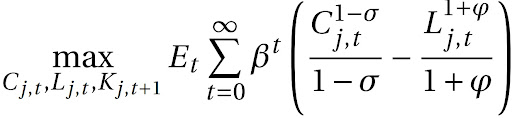
onde E_{t} é o operador de expectativas, \beta é o fator de desconto intertemporal, C é o consumo de bens, L é o número de horas trabalhadas, \sigma é o coeficiente de aversão ao risco relativo e \phi é a desutilidade marginal em relação à oferta de trabalho.
Tendo isso em vista, preservamos as seguintes equações:
1. A lei de movimento do capital:

2. A oferta de trabalho:

3. A Equação de Euler:

Agora, entramos no diferencial do modelo, que é o fato de que o setor produtivo é assumido possuindo uma estrutura de mercado de competição monopolística.
Firmas
O setor produtor da economia é dividido em duas partes: um setor de bens intermediários (empresas atacadistas) e um setor de bens finais (empresas varejistas). O setor de bens intermediários consiste em um grande número de empresas, cada uma produzindo bens diferenciáveis. Essas empresas devem decidir a quantidade de fatores de produção a serem usados e os preços de seus bens usando uma função de produção. No setor de bens finais, existe uma única empresa que, utilizando uma tecnologia específica e pertinente, agrega bens intermediários em um único bem que será consumido pelos agentes econômicos.
1. Empresas que produzem bens finais (empresas varejistas)
Numa perspetiva agregada, a concorrência monopolista, entre outros fatores, obriga-nos a reconhecer o fato de os consumidores comprarem uma grande variedade de bens, havendo necessidade, portanto, de modelos que assumam que os consumidores compram apenas um tipo de bem (uma cesta agregada com todos os bens). Este bem agregado (pacote de bens) é vendido por uma empresa de varejo dentro de uma estrutura de concorrência perfeita. Ou seja, assume-se que uma determinada empresa varejista é completamente idêntica a qualquer outra.
Supõe-se que seja possível representar um determinado bem de atacado em qualquer ponto dentro do intervalo [0,1]. Cada um desses bens é imperceptivelmente infinitesimalmente pequeno quando comparado à quantidade total de bens disponíveis. Portanto, assume-se que cada bem pertencente ao intervalo unitário é produzido por um único atacadista e é imperfeitamente substituível por qualquer outro bem. Assim, esses bens são produtos diferenciados, o que permite algum grau de poder de monopólio.
Para representar o problema que uma empresa de varejo enfrenta, sua tecnologia de produção e problema de maximização devem ser descritos. Desde a incorporação da ideia de competição monopolística na macroeconomia dominante nos anos oitenta e noventa, a forma funcional mais amplamente aplicada para a tecnologia de agregação é o agregador Dixit-Stiglitz (Dixit e Stiglitz, 1977):

onde Y_{t} é o produto dos varejistas no período t , Y_{j,t} para j \in [ 0, 1] é o bem de atacado j e \psi > 1 é a elasticidade de substituição entre os bens de atacado.
Com P_{t} como o preço nominal de um produto de varejo e P_{j,t} como o preço nominal de um bem de atacado j , o preço de cada bem no atacado é dado pelas firmas varejistas. Portanto, o problema da empresa varejista representativa é maximizar sua função lucro:
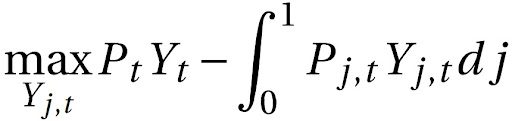
Substituindo o produto pelo agregador de tecnologia, temos:

Tomando as Condições de Primeira Ordem, temos:
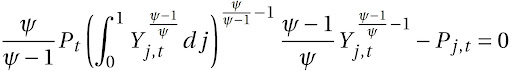
Ou:
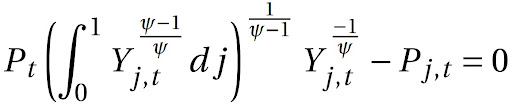
Lembrando que podemos reescrever o agregador de tecnologia da seguinte maneira:
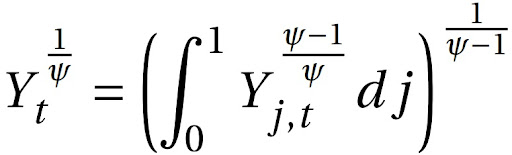
Consequentemente, substituindo o no nosso resultado, temos:

Rearranjando os termos e elevando-os por - \psi , temos:
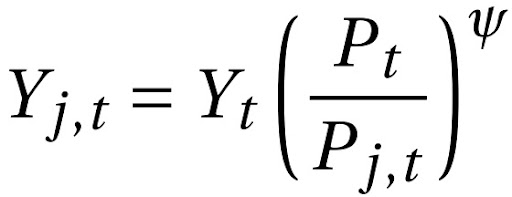
Essa expressão é a função de demanda do bem j no atacado, que é diretamente proporcional à demanda agregada Y_{t} e inversamente proporcional ao seu nível de preço relativo \frac{1}{\frac{P_{j,t}}{P_{t}}} .
Assim, substituindo o valor encontrado Y_{j,t} no agregador Dixit-Stiglitz, chegamos na seguinte expressão:
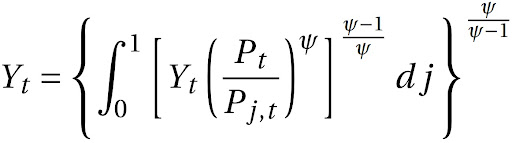
Fazendo manipulações algébricas, temos:

Isolando o termo do nível de preços:
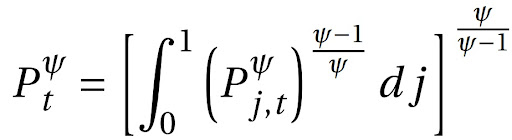
Consequentemente:

A equação acima é a regra de mark-up para bens finais (varejo).
2. Empresas que produzem bens intermediários (empresas atacadistas)
Para essa seção será necessário adotar algumas hipóteses, entre elas que devido à natureza diferenciada dos produtos atacadistas, as empresas atacadistas têm algum grau de poder de mercado e são, portanto, definidoras de preços (estrutura de mercado da concorrência monopolística). Supõe-se que não existam custos fixos de produção, logo o custo variável médio é igual ao custo total médio. Supõe-se também que o custo unitário de produção de um produto no atacado seja sempre o mesmo, independentemente da escala de produção. Isso significa que se supõe que as firmas atacadistas tenham retornos constantes de escala, resultando em um custo marginal de produção, independentemente da quantidade produzida.
A empresa de varejo resolve seu problema em duas etapas. Primeiro, a firma toma os preços dos fatores de produção (retorno do capital e salários) e determina a quantidade de capital e trabalho que usará para minimizar seu custo total de produção:

Sujeita à seguinte função de produção:

Com a seguinte lei de movimento da produtividade:

Em que A_{ss} é o valor da produtividade no estado estacionário, \rho_{A} é o parâmetro autoregressivo da produtividade, cujo valor absoluto precisa ser menor que um, |\rho_{A}| < 1 , para garantir a estacionariedade do processo, e \varepsilon_{t} \sim N(0,\sigma_{A}) .
Montando o Lagrangeano:

Tomando as condições de primeira ordem:
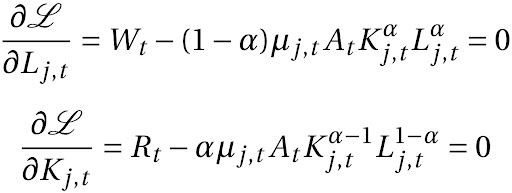
em que \mu_{j,t} = MC_{j,t} (MC: Custo Marginal).
Portanto as equações acima ficam:
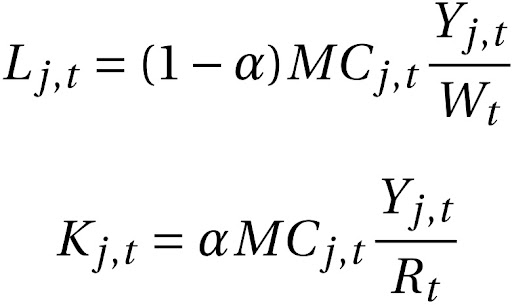
Essas duas equações representam a demanda de uma firma atacadista j por trabalho e capital, respectivamente.
Agora se faz necessário calcular as funções de custo total e marginal. O problema da firma é resolvido maximizando a função lucro, escolhendo os valores de cada insumo (L_{t} ,K_{t}):
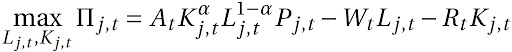
As condições de primeira ordem são as seguintes:

Portanto, chegamos nas usuais relações que se aprende sobre a teoria da firma nos cursos de microeconomia:

As equações acima representam a demanda por capital e trabalho, respectivamente, em que os custos marginais são iguais aos produtos marginais. Para achar o custo marginal, essas igualdades precisam ser combinadas:

O lado direito da equação é a taxa marginal de substituição técnica, que mede a taxa na qual o trabalho pode ser substituído por capital, mantendo um nível constante de produção. O lado esquerdo é a taxa econômica de substituição, que mede a taxa na qual o trabalho pode ser substituído por capital, mantendo o mesmo custo.
Rearranjando a equação prévia, temos:

Substituindo na função de produção, temos:
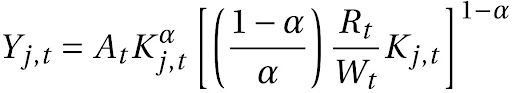
E, portanto:

Assim, substituindo o valor que achamos de K_{j,t} na equação de L_{j,t}, temos:
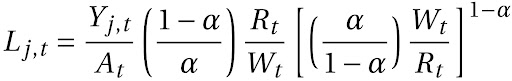
Fazendo mais substituições com base nas nossas equações prévias, temos:

Como o custo total é representado pela seguinte expressão:

então, com algumas manipulações algébricas, chega-se em:

Como o custo marginal MC_{j,t} nada mais é que o custo total dividido pelo produto ( \frac{TC_{j,t}}{Y_{j,t}} ), então temos que:

Com base nisso podemos prosseguir.
Precificação de Calvo
A segunda etapa do problema da empresa atacadista é definir o preço de suas mercadorias. A firma decide quanto produzir em cada período de acordo com a regra de Calvo (Calvo, 1983). Assim, a firma atacadista tem uma probabilidade \theta de manter o preço de seu bem fixo no próximo período e uma probabilidade 1 - \theta de definir seu preço de maneira ótima. Para este segundo tipo de firma, tendo definido o preço de seu bem em t , existe uma probabilidade \theta de que este preço permaneça fixo em t+1 , uma probabilidade \theta^{2} de que permaneça fixo em t+2 , e assim por diante. Consequentemente, a firma deve considerar essas probabilidades ao definir o preço de seu bem em t .
Adotando que a rigidez de preços segue a regra P_{j,t} = P_{j,t-1} , tem-se que o problema do atacadista capaz de reajustar o preço de seu bem é:
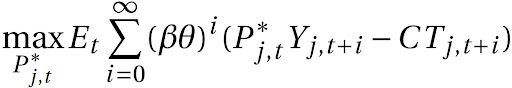
Substituindo Y_{j,t+i} pela expressão da função de demanda para o bem j no atacado, temos:
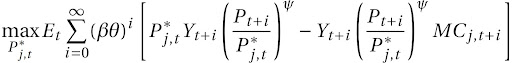
Tomando as condições de primeira ordem, temos:
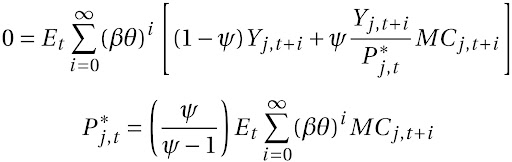
Observe que todas as empresas atacadistas que fixam seus preços têm o mesmo mark-up sobre o mesmo custo marginal. Assim, em todos os períodos, P^*_{j,t} é o mesmo para todas as 1 − \theta firmas que fixam seus preços. Combinando a regra de mark-up e o fato de que as empresas, dentro de seus respectivos grupos, usam os mesmos preços (já que estão sujeitas ao mesmo nível de tecnologia), o nível de preços agregado é obtido assim:

Consequentemente, o nível de preços geral é:
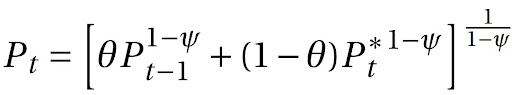
É importante lembrar que existe um continuum de firmas, e o grupo que pode alterar seu preço (assim como o grupo que não pode) é escolhido aleatoriamente, independentemente de quando cada firma alterou seu preço pela última vez. Isso significa que a distribuição de preços entre as empresas não muda entre os períodos.
Condições de equilíbrio do modelo
Ainda é necessário estabelecer uma condição de equilíbrio no mercado de bens. Tal condição será a seguinte:
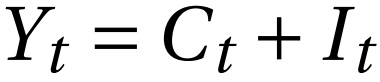
Tendo em vista essa equação, temos todas as equações para descrever a economia dentro do modelo. Sintetizamos elas na seguinte tabela:

Estado estacionário
Armados com a solução do modelo, o próximo passo é encontrar o estado estacionário, o ponto de origem das simulações que serão realizadas e o ponto de referência para a loglinearização. A ideia é que uma variável endógena x_{t} está em estado estacionário em cada período t . Isso ocorre se E_{t}x_{t+1} = x_{t} = x_{t−1} = x_{ss} . O primeiro passo é escrever o estado estacionário do modelo.
- Famílias

- Firmas

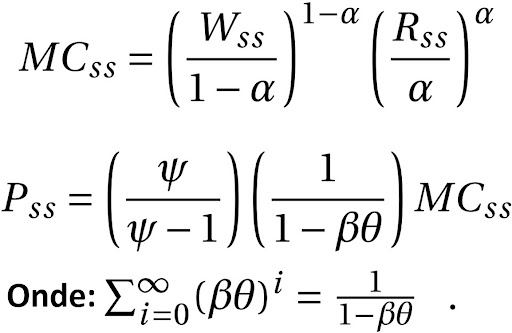
- Condição de equilíbrio

Inicialmente, devem ser determinados os valores dos preços P_{ss}, R_{ss}, W_{ss} e MC_{ss} . Desde que a função de excesso de demanda agregada seja homogênea de grau zero, os preços podem ser normalizados e as demandas expressas em termos de preço relativo e, como consequência, a soma dos preços normalizados deve ser sempre 1. Então tomemos o nível geral de preços como normalizado ( P_{ss} = 1 ). Os valores de R_{ss} e MC_{ss} também são conhecidos. Portanto, do estado estacionário que chegamos das famílias se segue que:

E do estado estacionário que chegamos das firmas se segue que:
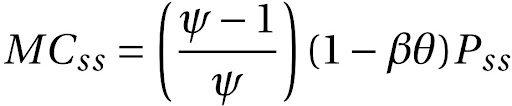
Com R_{ss} e MC_{ss} conhecidos, então o valor de W_{ss} também o é, dado que:

Determinados os valores dos preços, o próximo passo é determinar o equilíbrio nos mercados de insumos com o objetivo de obter as variáveis que compõem a demanda agregada ( C_{ss} e I_{ss} ). Portanto:

E temos que:

As expressões para investimento e consumo são obtidas. Por fim, para determinar o produto estacionário (Y_{ss}) , é necessário atender à condição de equilíbrio do mercado de bens. Sendo assim, temos que:

Rearranjando:

Consequentemente, nossos resultados obtidos para o estado estacionário são o seguinte:
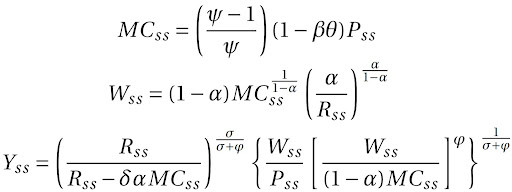

Consequentemente, para avaliar os choques no sistemas é preciso de microdados para estimar os parâmetros estruturais e fazer simulações, sendo este o procedimento padrão para os macroeconomistas fazerem suas previsões, seja no mercado financeiro ou no Banco Central. É possível através de um procedimento de loglinerização derivar a curva de Phillips novo keynesiana, que dita uma relação entre hiato-produto e a taxa de inflação. Entretanto, por razões de espaço, ficaremos por aqui.
Conclusão
A contra-revolução keynesiana ao golpe proferido pelo campo Novo Clássico com suas expectativas racionais permitiu que novamente os insights keynesianos com respeito aos ciclos econômicos prevalecessem na literatura no formato dos modelos DSGE. Munidos das expectativas racionais e dos modelos de competição monopolística e rigidez de preços, esse modelos permitem modelar ciclos gerados por flutuações na demanda agregada. Consequentemente, para muitos, apresentando um modelo mais fidedigno da realidade na medida que se adequa melhor aos dados. No presente texto, apresentamos uma versão simplificada do modelo, que por si só não é trivial.
Espero que tenham gostado e até a próxima.
Referências
Baqaee, David, and Emmanuel Farhi. The microeconomic foundations of aggregate production functions. No. w25293. National Bureau of Economic Research, 2018.
Blanchard, Olivier Jean, and Nobuhiro Kiyotaki. “Monopolistic competition and the effects of aggregate demand.” The American Economic Review (1987): 647-666.
Calvo, Guillermo A. “Staggered prices in a utility-maximizing framework.” Journal of Monetary Economics 12.3 (1983): 383-398.
Castro, Marcos R. de, et al. “SAMBA: Stochastic analytical model with a bayesian approach.” (2015).
Christoffel, Kai Philipp, Günter Coenen, and Anders Warne. “The new area-wide model of the euro area: a micro-founded open-economy model for forecasting and policy analysis.” (2008).
Costa, Celso. Understanding DSGE models: theory and applications. Vernon Press, 2018.
Dixit, Avinash K., and Joseph E. Stiglitz. “Monopolistic competition and optimum product diversity.” The American Economic Review 67.3 (1977): 297-308.
Fischer, Stanley. “Long-term contracts, rational expectations, and the optimal money supply rule.” Journal of Political Economy 85.1 (1977): 191-205.
Friedman, Milton, and Anna Jacobson Schwartz. A monetary history of the United States, 1867-1960. Vol. 14. Princeton University Press, 2008 [1963].
Fujiwara, Ippei, et al. “The Japanese economic model (JEM).” Monetary and Economic Studies 23.2 (2005): 61-142.
Galí, Jordi. Monetary policy, inflation, and the business cycle: an introduction to the new Keynesian framework and its applications. Princeton University Press, 2015.
Galí, Jordi. “The state of New Keynesian economics: a partial assessment.” Journal of Economic Perspectives 32.3 (2018): 87-112.
Gordon, Robert J. “What is new-Keynesian economics?.” Journal of Economic Literature 28.3 (1990): 1115-1171.
Mankiw, N. Gregory. “Small menu costs and large business cycles: A macroeconomic model of monopoly.” The Quarterly Journal of Economics 100.2 (1985): 529-538.
Phelps, Edmund S., and John B. Taylor. “Stabilizing powers of monetary policy under rational expectations.” Journal of Political Economy 85.1 (1977): 163-190.
Rotemberg, Julio J. “Sticky prices in the United States.” Journal of Political Economy 90.6 (1982): 1187-1211.
Rotemberg, Julio J., and Michael Woodford. “An optimization-based econometric framework for the evaluation of monetary policy.” NBER macroeconomics annual 12 (1997): 297-346.
Shapiro, Carl, and Joseph E. Stiglitz. “Equilibrium unemployment as a worker discipline device.” The American Economic Review 74.3 (1984): 433-444.
Stiglitz, Joseph E., and Bruce C. Greenwald. “Keynesian, New Keynesian and New Classical Economics.” (1987): 119-133.
Wickens, Michael. Macroeconomic theory: a dynamic general equilibrium approach. Princeton University Press, 2012.
.
Leia também:
A Teoria dos Ciclos Reais de Negócios
A Nova Economia Institucional e a Cliometria
Um toy model explicando como o Banco Central define a taxa básica de juros
Qual o juro de equilíbrio atual do Brasil?









Deixe um comentário