O modelo neoclássico de crescimento

A teoria do crescimento na ciência econômica tem como ponto de referência o clássico artigo “A contribution to the theory of economic growth” do economista nobelista Robert Solow. O artigo busca tentar responder a simples, mas nem um pouco trivial, pergunta fundacional das ciências econômicas: quais são as causas da riqueza das nações?

O economista, a título de aproximação, quis responder com um raciocínio básico: as firmas crescem quando produzem mais, ou seja, quanto mais capital e trabalho em uma produção, maior o produto e portanto maiores serão as taxas de crescimento. Ora, então o crescimento de uma nação deve ser função do estoque de capital e trabalho desta economia. Entender essa relação pode nos iluminar sobre outra pergunta relevante, que é porque alguns países são pobres e outros são ricos.

Colocando essa obviedade de que o crescimento de uma nação deve ser função do estoque de capital e trabalho no holofote da nossa investigação teórica e empírica, torna-se mais fácil o caminho a ser traçado pela pesquisa, pois cabe agora tentar entender a relação entre insumo e produto, assim como a dinâmica no qual o capital (e o trabalho) crescem com o tempo, e por sua vez a relação destas taxas com a taxa de crescimento da economia.

Em termos mais técnicos, a grande contribuição do Solow foi a especificação e estimação de uma função de produção agregada com uma forma funcional específica (a Cobb-Douglas). Tal função permitiu que se chegasse na taxa de crescimento per capita em estado estacionária como função de parâmetros estruturais da economia (no caso, a taxa de poupança, a quantidade de capital e assim por diante).

O resultado do artigo é o famoso modelo de Solow, no qual se prevê a taxa de crescimento da economia em função da quantidade de poupança, da contribuição do capital na produção e da taxa de depreciação do capital dessa economia. Além disso, prevê uma convergência nas taxas de crescimento dos diversos países em estado estacionário, isto é, quando as forças de crescimento se estabilizam.

Trata-se de um modelo elegante, mas limitado e com algum suporte empírico (para saber mais sobre tentativas de superação deste modelo, recomendo este link). O cerne deste modelo é encontrar a taxa de crescimento em função de parâmetros dados, sendo assim, não é possível estudar a dinâmica desses, muito menos os efeitos sobre o bem-estar da população. Esses problemas decorrem da ausência de microfundamentos ao modelo. O que quero dizer com isso é que o modelo simplesmente agrega os indivíduos e firmas da economia como entes representativos e a partir de restrições na alocação de recursos tenta achar a taxa de crescimento, sem modelar como estes mesmos agentes tomam suas decisões.

As críticas possíveis ao modelo de Solow podem ser estendidas para todos os modelos macroeconômicos agregados anteriores à crítica de Lucas (1976). O fundamental do que se tirou dessa crítica foi a necessidade de endogeneizar os parâmetros estruturais, ou, em outras palavras, a partir da teoria micro de como agentes tomam decisões é preciso gerar a teoria macro, assim explicando os fenômenos que abrangem toda a economia como sendo fundamentados na ação de agentes individuais.

Eis que surge a macro moderna, que fala menos de agregação e mais em dinâmica e equilíbrio geral. Modelos são construídos a partir de fundamentos micro, no qual são modelados explicitamente características e objetivos dos agentes, estrutura de mercado, informação, tecnologia, etc. Analisam-se agentes racionais que querem maximizar seu bem-estar dadas as restrições que enfrentam, sendo o comportamento agregado uma consequência de decisões individuais e da estrutura da economia. Segue-se a isso uma abordagem de equilíbrio, no qual os agentes interagem em mercados nos quais preços e quantidades são determinados em equilíbrio.

Mas o que se ganha com essa abordagem? Em primeiro lugar, consistência interna dado que as variáveis agregadas são consistentes com decisões individuais, rigorosamente fundamentadas em um nível microeconômico. Em segundo lugar, transparência, pois as hipóteses são explicitamente definidas. Além disso, é possível a análise de políticas públicas a partir de uma análise de bem-estar de cada agente. Possível determinar como agentes reagem à introdução de novas políticas, assim superando a crítica de Lucas. (Para saber mais sobre isso, e sobre a história da macroeconomia em geral, recomendo este texto).

Uma vez que se percebe a necessidade de ultrapassar os modelos antigos, tal qual o de Solow, então o que fazer? Essa resposta foi dada de maneira independente pelos economistas Frank Ramsey (1928), David Cass (1965) e Tjalling Koopmans (1965), que buscam modelar a trajetória ótima de poupança baseada nas decisões (preferências) dos agentes na economia. No caso do modelo em questão, que ficou conhecido como Modelo Neoclássico de Crescimento ou Modelo Ramsey-Cass-Koopmans, busca-se entender a pergunta de Solow com base na teoria microeconômica. Então, ao modelo.

Sumário

O Modelo Neoclássico de Crescimento ou Modelo Ramsey-Cass-Koopmans

A economia é modelada como sendo composta por um domicílio representativo e uma única firma representativa, na qual ambos os agentes são tomadores de preços. A firma combina os insumos capital e trabalho de maneira a produzir os bens desta economia. A relação entre capital e trabalho para produto é chamada de função de produção, que é descrita de maneira não paramétrica pela seguinte equação:

As hipóteses que tomamos em relação a essa função são as seguintes:

1. Retornos constantes de escala:

Ou seja, ao dobrarmos (ou multiplicarmos por um escalar qualquer) os insumos, o produto cresce na mesma proporção.

2. Produto marginal positivo:

Ou seja, quando se varia uma unidade do insumo, o produto varia positivamente. Então mais insumo na margem, mais produto na margem.

3. Produtividade marginal decrescente:

Ou seja, por mais que na margem o produto cresça com o aumento marginal de um dos insumos, esse crescimento é decrescente. Isto é, colocar mais uma unidade de insumo faz crescer X a mais de produto, colocar ainda mais insumo faz o produto crescer Y, em que Y < X.

4. Condições de Inada:

Ou seja, quando mais se coloca do insumo, mais a produtividade marginal daquele insumo se aproxima de zero; analogamente, quanto menos se coloca do insumo, mais a produtividade marginal daquele insumo se aproxima de infinito.

A dinâmica do crescimento do capital nessa economia é descrita pela seguinte equação no qual a taxa de depreciação é representada por $\delta \in (0, 1)$ :

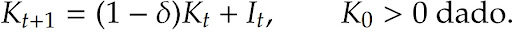
Vamos assumir, a título de simplificação, que a economia é fechada (não faz troca com outros países) e não há governo (não há impostos nem gastos governamentais). Parecem simplificações absurdas, mas elas não afetam o entendimento dos mecanismos essenciais operando no crescimento, sendo assim, é uma mera simplificação analítica:

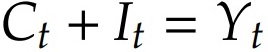
A restrição de recursos na economia então é descrita da seguinte maneira:

A lógica desta equação é simples: a produção de um período é alocada para três finalidades possíveis: (i) consumo; (ii) formação de capital para o período seguinte; (iii) reposição do capital depreciado no período corrente. Uma vez que eliminamos a possibilidade de trocas internacionais, então tudo que é consomido, poupado, investido e produzido vem da própria economia doméstica.

Tendo descrito as característica principais da economia podemos ir às escolhas dos agentes econômicos:

Problema da firma

Modelamos a firma representativa como buscando maximizar seu lucro, sendo o problema clássico da teoria da firma microeconômica, isto é, a firma busca seu maior lucro sujeita à sua função de produção, que representa aqui sua restrição.

Esta equação nos mostra que a firma busca produzir o máximo, tomando que o custo de alugar capital é taxa de aluguel de capital multiplicada pelas unidades que comprou deste insumo, assim como o custo de contratar mão-de-obra é o número de empregados multiplicado pelo salário. Vamos assumir que o preço do bem produzido é 1 para facilitar as contas.

Resolvendo este problema de otimização restrita chegamos que as condições de primeira ordem são as seguintes:

A taxa de aluguel do capital é igual à produtividade marginal do capital, isto é, o acréscimo na margem de produto com uma unidade a mais de capital é igual a taxa de aluguel, o que implica que o quanto a firma gasta pelo acréscimo de capital é justamente o acréscimo marginal que ela produz com esse capital. Sendo assim a remuneração do capital é função de sua produtividade. A mesma lógica vale para o salário, que se iguala à produtividade marginal do trabalho. Uma maneira intuitiva de pensar esses resultados é que em um mercado competitivo você ganha exatamente igual a sua produtividade.

Problema do consumidor

Seguindo o modelo canônico de microeconomia, os agentes econômicos possuem preferências, que se forem consistentes podem ser representadas via uma função chamada função utilidade (para ler mais sobre isto, recomendo este link). O problema do consumidor é escolher a cesta de bens que lhe provê maior utilidade dentro do seu orçamento, afinal sua renda não é infinita.

Todavia, ao considerar questões de crescimento, passamos a envolver questões temporais nas decisões dos agentes. Neste cenário, o indivíduo que estamos considerando na nossa economia não só escolhe o quanto vai consumir hoje e poupar (consumir amanhã), porém também tem de escolher hoje entre consumo e lazer, isto é, entre o período que trabalha (consome) e o período em que não trabalha (lazer). O trade-off entre consumo hoje e amanhã é o problema de escolha intertemporal, enquanto que o trade-off entre renda e lazer é o problema de escolha intratemporal.

Comecemos com a escolha intertemporal: naturalmente, os indivíduos escolhem com base na sua renda, mas é um erro pensar que estes consideram apenas a sua renda corrente. Na verdade, a decisão de consumir e poupar depende do presente e do que se espera para o futuro. Para simplificar a análise, consideramos um consumidor que vive somente dois períodos: juventude e velhice. Existe um único bem de consumo na economia e em cada período o consumidor tem uma dotação do bem (renda) e decide quanto consumir.

Período 1: renda y₁ (bens) e consumo c₁.
Período 2: renda y₂ (bens) e consumo c₂.

y também é chamado de dotação, ou renda em bens.

O consumidor pode pedir um empréstimo e poupar a uma taxa de juros real r.

Dessa forma, a poupança no período 1 é descrita pela seguinte equação:

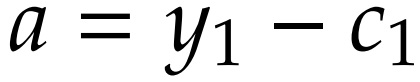
Sendo a o valor em bens da poupança. Se a < 0, o consumidor pede um empréstimo. Naturalmente, o indivíduo não quer poupar no 2° período. Assumimos que também não pode pedir emprestado, pois se pudesse pedir emprestado no último período de vida, pediria o máximo possível, pois não precisará repagar no período seguinte.

No segundo período, a restrição orçamentária é:

Agrupando consumo e renda:

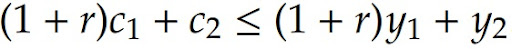
Se c₁ se reduz em 1 unidade, c2 pode aumentar em 1 + r unidades. Portanto, tendo em vista a equação acima, podemos chegar na restrição orçamentária intertemporal dos indivíduos:

Graficamente a restrição orçamentária pode ser representada da seguinte maneira:

Agora, com relação às preferências dos indivíduos, assumimos que elas possuem esta função de utilidade:

Em que $0 < \beta < 1$ é um fator de desconto, mede a impaciência. Assumimos como de costume que u’ > 0, i.e., mais consumo em qualquer período é melhor; u’’ < 0, i.e., a utilidade marginal é decrescente ou, em outras palavras, os ganhos de utilidade ao consumir a segunda ou mais unidades de um bem são menores do que os ganhos de utilidade ao consumir a primeira unidade. Além disso, tomamos que os indivíduos preferem consumir certa quantidade nos dois períodos a consumir essa mesma quantidade em um só período, ou seja, os agentes gostam de cestas balanceadas, sem extremos de um bem ou outro.

Assim temos o clássico problema do consumidor, só que agora considerando o fator temporal. Portanto podemos representar este problema pela seguinte equação:

Desse problema chegamos na clássica equação de Euler:

Graficamente chegamos no seguinte resultado:

A taxa marginal de substituição (TMS) se iguala aos preços relativos. Ou seja, a taxa pela qual um indivíduo sacrifica consumo futuro por uma unidade de consumo presente é igual a taxa de juros mais um.

Antes de continuarmos, é preciso ter noção de algumas definições. Como a escolha entre renda e lazer envolve o quanto se vai trabalhar, é necessário ter uma noção sobre as definições econômicas em relação ao mercado de trabalho, Vamos às definições:

Empregados: indivíduos que trabalharam no último período.
Desempregados: indivíduos que não trabalharam no último período, mas procuraram emprego.
Fora da força de trabalho: indivíduos que não trabalharam nem procuraram emprego no último período.

Assim, temos as seguintes equações:

Força de trabalho = Empregados + Desempregados;
Taxa de participação = Força de trabalho/População;
Taxa de emprego = Empregados/População;
Taxa de desemprego = Desempregados/Força de trabalho = 1 – (taxa de emprego/taxa de participação).

Tendo essas definições em mãos, podemos ir ao modelo de escolha intratemporal.

O indivíduo escolhe entre consumo e lazer e ordena as alternativas de acordo com a seguinte função de utilidade:

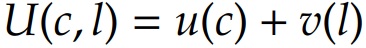
Sendo u e v crescentes e côncavas (ou seja, a utilidade marginal é positiva e decrescente). Assumimos que o indivíduo tem 1 unidade de tempo normalizado a ser dividida entre trabalho e lazer: $l \in [0, 1]$ . Portanto, a oferta de trabalho é:

O indivíduo escolhe exatamente quanto quer trabalhar e toma o salário real w como dado. Sua restrição orçamentária, portanto, é:

Perceba que w é o preço relativo entre lazer e consumo: abrir mão de uma unidade de lazer permite comprar w unidades de bens. Graficamente a restrição fica representada desta maneira:

Isto posto, podemos representar o problema de escolha intratemporal com a seguinte equação:

A resolução deste problema de otimização restrita nos provê as seguintes equações de primeira ordem:

Esta solução nos diz que a taxa pela qual o indivíduo troca consumo e lazer é igual ao preço relativo desses bens. Isto é, a taxa pelo qual o indivíduo sacrifica uma unidade de consumo por lazer se iguala ao seu salário. Intuitivamente, quanto maior seu salário, mais ele sacrifica trabalho para consumir lazer. Graficamente, esta solução é a seguinte:

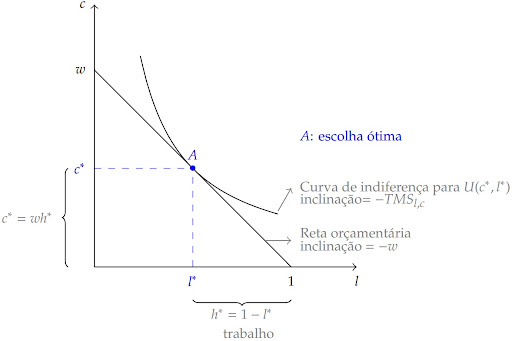
Uma vez que contemplamos os dois problemas de escolha que os indivíduos tomam inter e intratemporalmente, podemos juntar ambos em um único problema, que os indivíduos enfrentam no mercado:

O indivíduo quer maximizar sua utilidade, que neste caso significa escolher a quantidade ótima de consumo hoje, trabalho/lazer e consumo amanhã (poupança), ou seja, uma escolha de consumo ao longo de toda sua vida. Note que uma vez que estendemos nossa análise intertemporal para além de dois períodos é necessário colocar uma restrição a mais, que é a chamada condição Não-Ponzi.

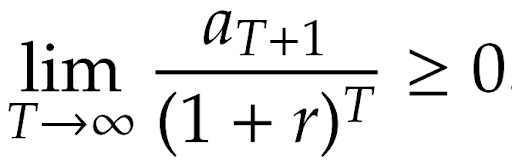
Essa restrição está meramente nos dizendo que não é possível fazer um esquema de Ponzi, isto é, acumular dívida que será rolada para sempre com mais endividamento. Dada a possibilidade de insolvência, o agente precisa efetivamente pagar o que se endividou. Esta restrição vale tanto para indivíduos quanto para governos.

Ao resolvermos o problema do indivíduo temos as soluções usuais já comentadas:

No caso vale ressaltar aqui que r_t+1 é a taxa de juros entre os períodos t e t+1. Em linhas gerais, vale a seguinte regra de bolso: a taxa marginal de substituição intertemporal se iguala ao juros, enquanto a taxa marginal de substituição intratemporal se iguala ao salário. De maneira ainda mais geral, a taxa marginal de substituição se iguala sempre aos preços relativos, pelo menos quando estamos considerando escolhas em um mercado competitivo.

A solução encontrada tanto no problema da firma quanto no problema do indivíduo é aquela que equilibra os mercados. Ou seja, no mercado de bens temos a seguinte condição de equilíbrio:

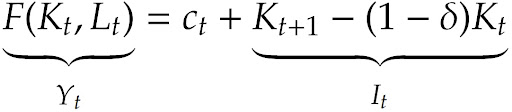
No mercado de trabalho temos a seguinte condição de equilíbrio:

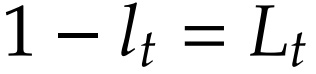
No mercado de capitais temos a seguinte condição de equilíbrio:

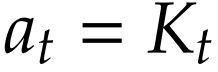
Ou seja, no equilíbrio de mercado, a oferta se iguala à demanda. Tendo dito isso, agora podemos caracterizar o equilíbrio da economia. Primeiro, encontramos os preços que equilibram os mercados para depois usarmos os preços para encontrar as alocações.

Vamos relembrar as soluções do problema da firma:

Firmas demandam K e L até que seus preços se igualem aos produtos marginais, F_K(K, L) e F_L(K, L). Vale ressaltar também que, como a_t = K_t, a taxa de juros é o retorno líquido do capital:

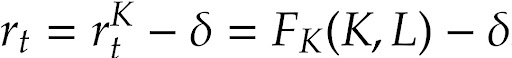
Assim, substituindo esses preços nas demais equações chegamos as seguintes alocações:

Portanto, em um mercado competitivo a solução de mercado (do modelo de crescimento neoclássico) são os seguintes resultados:

O indivíduo está restrito pelos preços relativos e, em equilíbrio, os preços refletem a tecnologia. O resultado apresentado demonstra a eficiência do mercado competitivo, uma vez que as alocações e preços são aqueles que esgotam os termos de troca, i.e., não é possível melhorar uma alocação para um indivíduo sem piorar a de outro. Por isso, caracterizamos estas alocações como Pareto-Eficiente.

Dinâmica do modelo

Aqui temos uma economia com população constante. No modelo de Solow, com poupança constante, essa economia converge para um estado estacionário. Então cabe a pergunta: como se comporta a economia com poupança endógena? Para respondê-la vamos simplificar a economia de modo a focarmos na decisão de consumir de poupar/investir.

Eliminaremos a decisão de trabalhar, assim como a utilidade dependendo apenas do consumo. Nesse caso, L_t = 1 − l_t = 1. O capital agregado é igual ao capital por trabalhador: K_t = k_t. Além disso, considere que a utilidade do indivíduo representativo tem a seguinte forma funcional:

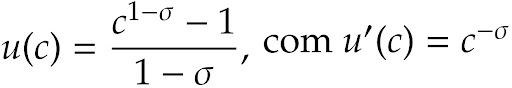
O que implica que a equação de Euler fica da seguinte maneira:

Esta equação relaciona a taxa de crescimento do consumo entre t e t + 1 com o nível do capital em t + 1. Estoque de capital baixo implica em crescimento alto do consumo. K baixo implica produtividade F_K alta que por sua vez implica preço de equilíbrio r^K alto, que acarreta numa taxa de juros de equilíbrio $r^K - \delta$ alta e assim o consumo presente é caro frente ao consumo futuro.

Agora em relação à dinâmica do capital temos a seguinte restrição:

Esta equação, por sua vez, relaciona capital futuro, capital corrente e consumo. Implica que mais consumo corrente leva a menos investimento e menos capital no futuro.

Juntando essas dinâmicas temos o seguinte diagrama de fases:

A linha vertical da figura representa consumo constante, que é o que se espera no estado estacionário. Assim, dada essa condição, podemos desdobrá-la nas nossas outras soluções de modo que chegamos no seguinte resultado:

Acima, tomamos $\beta = 1/(1 + \rho$ , em que $\rho$ é a taxa de desconto do indivíduo. Vale notar que o nível de capital que satisfaz a equação acima é apenas K_ss , isto é, o estoque de capital em estado estacionário. A taxa de juros que mantém c constante é:

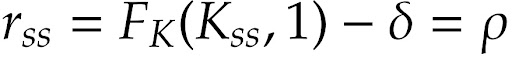
A taxa pela qual a economia desconta o futuro (r) se iguala à taxa pela qual o indivíduo desconta o futuro ( $\rho$ ).

Logo temos a seguinte dinâmica: se o estoque alto de capital estiver acima do estoque em estado estacionário, K > K_ss , isso faz com que c_t+1/ c_t< 1; assim, tem-se produtividade baixa, juros baixos (r < r_ss), e portanto consumo caindo. Agora, se o estoque baixo de capital estiver abaixo do estoque em estado estacionário, K < K_ss , isso faz com que c_t+1/ c_t> 1; assim, tem-se produtividade alta, juros altos (r > r_ss), e portanto consumo subindo.

Dada a dinâmica do consumo, é preciso olhar a do capital, representada pela curva vermelha no diagrama de fases. Esta curva representa o capital constante e este só será constante se:

Esse é o consumo necessário para que o investimento seja suficiente apenas para repor o capital depreciado:

Portanto, temos a seguinte dinâmica do capital:
(i) Consumo alto (acima da curva) (K_t+1 < K_t); isto é, muito consumo e pouco investimento, dado que $I < \delta K$ , implicando que o capital está caindo.
(ii) Consumo baixo (abaixo da curva) (K_t+1 > K_t); isto é, pouco consumo e muito investimento, dado que $I > \delta K$ , implicando que o capital está subindo.

A interseção das curvas representa o estado estacionário, ou seja, o equilíbrio de longo prazo do crescimento desta economia se dá na intersecção das dinâmicas do capital e do consumo pelo tempo, com capital por trabalhador constante k_ss = K_ss , dado por:

E consumo per capita constante c_ss dado por:

Preços de equilíbrio são constantes em estado estacionário, sendo o preço do capital dado por:

O salário é dado por:

E a taxa de juros é dada por:

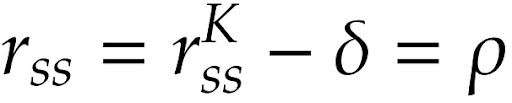
Suponhemos que a função de produção agregada da economia possa ser descrita por uma função Cobb-Douglas,

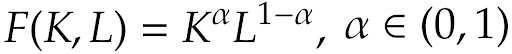
Neste caso, temos que o capital em estado estacionário é o seguinte:

Assim, graficamente, nosso modelo, tal qual o modelo de Solow, prevê uma convergência nas taxas de crescimento. Entretanto, no modelo neoclássico há uma região específica para tal convergência acontecer, que pode ser representada pelo diagrama de fases:

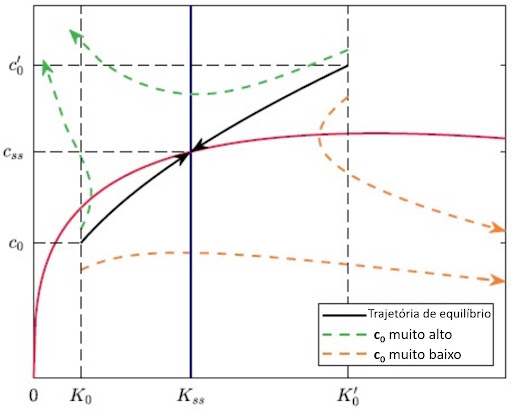
Desta forma, concluímos o modelo representando o crescimento econômico como função de parâmetros estruturais da economia rigorosamente microfundamentados. Para entender mais da matemática por trás, se faz necessário estudar Cálculo Diferencia e Integral, assim como Microeconomia (além de, obviamente, Macro). Aa longo do texto, seguimos bem de perto a exposição do livro de Kurlat (2020) . Espero que tenham gostado e até a próxima!

Referências

Cass, David. “Optimum growth in an aggregative model of capital accumulation.” The Review of economic studies 32.3 (1965): 233-240.

Koopmans, Tjalling C. “On the concept of optimal economic growth.” (1963).

Kurlat, Pablo. 2020. “A Course in Modern Macroeconomics,” publicado independentemente.

Lucas Jr, Robert E. “Econometric policy evaluation: a critique”, in K Brunner and A Meltzer (eds.), The Phillips Curve and Labour Markets, Carnegie-Rochester Conference Series on Public Policy, Vol. 1, Amsterdam: North-Holland.” (1976).

Solow, Robert M. “A contribution to the theory of economic growth.” The quarterly journal of economics 70.1 (1956): 65-94.